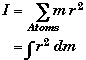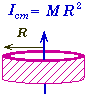• 

 

Rotational dynamics

 

 

---

 

Rotational dynamics

 

The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.

We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge

Physics

 

Rotational dynamics

 

Everything you need to know about Rotational Dynamics: (Fixed Axis)

 

 

Moment of Inertia:

*The moment of inertia of a system about some rotational point is the measure of an object's resistance to a change in the object's angular acceleration due to the action of a torque.
* The moment of inertia depends upon how an object's mass is distributed relative to it pivot point.

For a solid dm = r dV where r is the density function and dVis a differentially small volume.
* A body does not have just one moment of inertia but potentially an infinite number of I's, one for every different pivot point.
* For a fixed pivot point, an object has only one value for its moment of inertia independent of the torques acting on it. In other words, the torque acting on a body does not affect its moment of inertia.

Units:
SI: kg m2

 

Parallel-Axis Theorem:

There is a simple relationship between the moment of inertia about the center of mass of a body Icm and the moment of inertia about some other point that is a distance dfrom the center of mass provided both axes of rotation are parallel.

* If you know the moment of inertia about the center of mass you, can find it about ANY pivot point by using the parallel axis theorem, provided the axis of rotation is parallel.

 

 

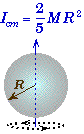
Moment of Inertia of Simple Solids:

 

Moment of Inertia Examples

Sign Convention: Clockwise Torques are Positive

Solid cylinder of mass M1 and radius R1rotating pivoted about its center:

Two solid cylinders stuck together with forces applied tangentially to their edges:

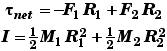A horizontal bar with a mass M pivoted about one end with a small mass m1attached to the other end.

A horizontal bar of mass M pivoted about its center with two different masses attached to the ends of the bar.

Rotational Kinetic Energy (Kr)
Rotational Kinetic energy is the energy of rotation.  It depends only upon the square of the angular speed and the Inertia of the object.  For example, the Disks rolling in Exploration 1 had rotational kinetic energy while it was rolling, but if the same disk were to slide across the table it would have zero rotational kinetic energy.

Rotational Kinetic Energy
Kr = ½ I w2 
Change in Kinetic Energy
DK = Kr - Kro =  ½ I w2  -  ½ I wo2
Rolling Marble Problem

A solid marble with a radius of 2.60 cm and a mass of 370 grams is rolling along the ridge of a hill that is 58.0 cm high. Initially the sphere is observed to revolve 15 times every second just before it encounters a downhill section. If the marble rolls without slipping, and the energy lost due to rolling friction is negligible:
(A)	What is the sphere's initial mechanical energy ? Initially, what fraction of the sphere's mechanical energy is potential energy, kinetic energy, and rotational energy ?
(B)	Show that the ratio of the marble's kinetic energy to its rotational energy is constant throughout its motion.
(C)	What is the maximum height that the marble could roll up an elevated section ?
(D)	How fast will the marble be moving when it reaches the bottom of the hill ?

 

Sketch and Process:

A marble rolls without slipping along an undulating surface.
Givens and Labels:

 

Relevant Physics:
For a freely rotating body the total mechanical energy is conserved.

This means that if we can find the mechanical energy at some point along the marble's path, then we know the marble's ME at all other points along its path. Since we know something about the marble's initial motion and position, we can find the initial ME.
Since the marble is rolling without slipping, then its angular velocity is related to the linear velocity of its center of mass,

(A) Find MEo.
We really do not need a separate symbol to distinguish the marble's initial mechanical energy MEo from the ME at any other point, since the mechanical energy is energy is conserved.

To determine the KEo we need to determine the marble's initial velocity. Since the marble's velocity is just the velocity of its center of mass, and the ball is rolling without slipping,

Then

To determine the REo we need to determine the marble's moment of inertia I. Since the marble is a solid sphere,

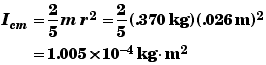
Then

We already have the value of all the quantities we need to determine PEo relative to its position when it is at the bottom of the hill. We do not need to worry about the fact that the center of mass of the ball is 2.60 cm above the track since the center of mass is also 2.60 cm above the track at the bottom or any place else along the track.

The total energy is the sum of the kinetic, potential, and rotational energy.

The fraction of mechanical energy that is KE, RE, and PE is simply their ratio.

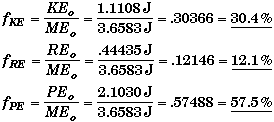
(B) Find KE / RE at any point.
Since the marble is rolling without slipping, then v = w t at any point.

For any object that rolls without slipping there is a fixed ratio between the KE and the RE , because there is a fixed relationship between the object's linear speed and its angular speed.
The ratio of the KE to PE will not be constant, since the ball's velocity and height are not necessarily related.
(C) Find hmax.
When the ball reaches its highest point, it will come to a halt and stop rolling. All of its ME will be PE. At its highest point,

An alternate symbolic solution is,

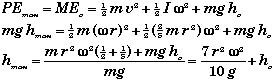
Thus the maximum height does not depend upon the mass of the marble. A marble of any mass which has the same radius would go to the same height under the same starting conditions. This means that this part of the problem could have been stated without specifying the marble's mass. If the mass was not given then you would have to solve the problem symbolically to find hmax.
(D) Find vb , the velocity of the marble at the bottom.
At the bottom the marble's PE is zero since we chose this level as our reference frame. The marble has both KE and RE at the bottom, the sum of which will be equal to the marble's ME.

Since the marble is rolling without slipping, vb = wb r.

 

 

TORQUE -- "The Rotational Force"

 

*Torque plays the same role in problems involving rotational motion that Force plays in problems involving linear translational motion. Definition
*It is Torque that causes a system to rotate about its center of mass. It is Force that causes the center of mass of a system to accelerate.
*The Net Torque on a system causes the system to have an angular acceleration about its center of mass (or about its pivotal point if the system has a fixed axis of rotation). Newton's Second Law for Rotation :

* The Net Torque is the sum of all torques acting on a system about the pivot point.

* In rotational problems you will have to decide which direction, clockwise or counterclockwise, will be taken to be the positive direction.
* To determine the direction a torque acts, CW or CCW, envision a situation in which the only force acting on the system is the force creating the individual torque under consideration. The direction that the system would rotate due to that force alone is the direction of the torque created by that force.
Definition of Torque:
The Torque on an object about some pivot point is due to the action of a force on the object.
Magnitude of the Torque:
t = "Force" times the "Lever Arm"
= (Component of the Force perpendicular to Lever Arm) x (Lever Arm - the distance between the pivotal axis and the point where the force is applied) = Fp l

= (Force) x (Perpendicular line of action lever arm - the shortest distance between the pivot point and the line of action of the force through the body) = F lp

= (Force) x (Lever Arm) x sin(angle between the two) = F l sin(q)


Direction of Torque:

• The more exact definition is that the torque is that the torque is the cross product of the lever arm with applied force.
• The torque's direction is perpendicular to both the direction of the lever arm and the direction of the force. The direction can be found using the right hand rule.

SI Units: N m
* These are the same units as a Joule, but nobody uses Joules. There must be some deep connection which nobody has yet discovered. Any ideas ?
Same Torque Example:
* Forces that lie along the same line have the same perpendicular lever arm lp .
* A given force Fwill produce the same torque on a system if it is applied anywhere along a straight line. Here the perpendicular distance lp between the line of action of the force and the center of rotation will be the same.

Zero Torque Example:
All forces whose direction passes through the axis of rotation produce no torque on the system, no matter how large the magnitude. In such cases, the lever arm is zero, l = 0, or alternately there is no perpendicular component, Fp = 0, when line of action of the force passes through axis of rotation

Angular Momentum:
The angular "persistence or umph" of a rotating system
Definition:
For a group of interacting particles or a rigid body.

This is the vector cross product of each particle's radius vector from the point of rotation crossed with the momentum of the particle. For a freely rotating group particles the point of rotation would be the center of mass of the group.
For a single particle the magnitude of a particle's angular momentum can be expressed as:

Angular Momentum of a Rigid Body about a Fixed Axis:

Direction:

Units:
SI: kg m2/s

Conservation of Angular Momentum:
* A rotating system will keep on rotating unless acted upon by an external torque.
* If the net external torque on a system is zero, then both the magnitude and direction of the of a rotating system remains constant. If tnet = 0 then L = constant.

* Any force whose line of action passes through the axis of rotation of a system cannot create a torque on the system and cannot change the system's angular momentum.
* A rotating system can change its state of rotation without have any external agent acting on it if the system can change its moment of inertia by rearranging its distribution of mass internally. A spinning ice-skater who pulls in their arms is a classic example of an internal change in the moment of inertia.

Puck - Stick Collision Problem

A student places a light, 800 g plastic two-meterstick on an air hockey table. She shoots a 300 g air-puck at a speed of 4.00 m/s towards the stationary two-meterstick in such a way that the puck impacts the two-meterstick at an angle of 900. With a little practice, she finds that if the air-puck impacts the two-meterstick at just the right distance from its center, she is able to create a collision in which the air-puck comes to a stop and the two-meterstick goes rotating off. Assuming that there is no friction between the table and the puck or the two-meterstick:
(A)	Is angular momentum conserved during this collision ? What is the angular velocity of the two-meterstick after the collision if the puck strikes the two-meterstick at a distance of 50.0 cm from the center of the two-meterstick and the puck comes to a complete stop ?
(B)	Is linear momentum conserved during this collision ? Determine the final velocity of the center of mass of the two-meterstick if the puck come to a stop. Does the linear velocity of the meterstick depend upon where the puck strikes the meterstick ?
(C)	Is energy conserved if the puck strikes the two-meterstick 50.0 cm from its center and the puck comes to a stop ? What is the fractional energy loss during the collision ?
(D)	Determine the distance from the center which the puck must strike the two-meterstick for the puck to come to rest and energy to be conserved.

 

Sketch and Process:

A moving puck collides with a stationary two-meterstick at 900 on a frictionless surface. The distance the puck strikes the two-meterstick from its center is such that the puck comes to a halt during the collision.

 

Relevant Physics:
Since there are no external forces or torques on either body in the system, the linear momentum and the angular momentum will be conserved. Mechanical Energy could be conserved, but we cannot be sure because mechanical energy could be lost due to deformation of the bodies, energy in the form of sound, or ultimately energy in the form of heat.

 

Conservation of Angular Momentum:
The two-meterstick will under go free rotation about its center of mass after the collision. Thus we choose the center of mass to be the axis of rotation and the origin.
Just before the collision, the angular momentum of the puck is that of a point mass at a distance d from the center of rotation - the center of the stick.

We could also find this from

This is the angular momentum of the puck at any time before the collision.
Using this in the conservation of angular momentum.

Since the bar will be rotating freely Is is the moment of inertia of a thin bar about its center of mass.

In terms of the key variables of the problem, the conservation of angular momentum gives us a relationship between the initial velocity of the puck vo , the final angular velocity of the meterstick ws, and the location on the meterstick where it is struck d .

Conservation of Momentum:
The conservation of linear momentum applies to the center of mass motion of the two bodies. Thus we do not have to be concerned with the angular rotation of the meterstick, but only with its linear velocity.

Note that the meterstick is not a rolling body so we cannot use vs = (L/2) ws to find ws knowing just vs. This relation would be true if the meter stick was pined so that is could only rotate about its center of mass.

Conservation of Energy:
After the collision, the meterstick will have both rotational and kinetic energy.

The three conservation laws give us three equations,

with four possible unknowns vs, ws, d, and Eloss.

 

(A) Find ws knowing that d = 50 cm.
The only way angular moment would not be conserved would be if the two bodies were not isolated, and some external force, like friction, acted on them. Even if friction were present, the collision time is so small that the action of friction on the bodies during the collision time would also be small. Friction would have more effect on the motion of the bodies before and after the collision than during the collision. Any results we find in this problem will be a better approximation for the state of the puck and meterstick immediately before and after they collide.
In the relevant physics, we found the angular momentum of the puck about the center of mass of the meterstick, so that

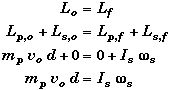
Solving for ws,

The minus sign means that the two-meterstick will rotate CCW (counterclockwise) about its center.

(B) Find vs when d = 50 cm.
Like angular momentum, linear momentum will also be conserved since the effects of any external forces are assumed to be small. The conservation of linear moment for the center of mass of the two bodies is given by,

From this we can solve for the final velocity of the two-meterstick.

The minus sign means the meterstick is moving to the left after the collision.
If the puck stops, then all the momentum it had must be transferred to the meterstick. The only way the meterstick can have this much momentum is if it is moving at 1.50 m/s in the same direction as the puck was moving. Thus the meterstick's linear velocity does not depend upon where the meterstick was struck, but only upon the velocity of the puck and the masses of the two bodies. Mathematically, you could also deduce this from the fact that the above equation does not depend upon the variable d. We saw from part A that the location of where the meterstick is struck determines the meterstick's angular velocity of rotation.
(C) Find Eloss when d = 50 cm.
We saw in part A and B, that the conservation of linear momentum and angular momentum uniquely determine the meterstick's final motion. Thus we can determine the final mechanical energy of the system and see how it compares with the initial mechanical energy.

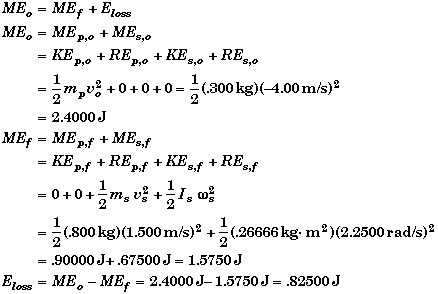
The fractional energy loss is just the ratio of the energy loss to the initial energy,

Energy is not conserved. It could be if the meterstick was struck in a different location d from the center of mass.
(D) Find d when ME is conserved.
First assume that the mechanical energy is conserved, and plug in the results found for the conservation of linear and angular momentum in parts A and B.
Conservation of Angular Momentum:

Conservation of Linear Momentum:

Conservation of Energy:

Note that not every combination of the puck's mass and the meterstick's mass will produced a location where this point would be on the meterstick. This will occur when,

When the mass of the two-meterstick is greater than four time the mass of the puck, then there will be no way to conserve energy.

 

Newton's Second Law for Rotation:
There are three forms. The most useful in problem-solving is the rotational equivalent of ,

 

 

A second is the relations between force and momentum, . The rotational equivalent is that any change in a system's angular momentum is caused by a net torque acting on the system.

The third involves the angular analog of linear impulse . The rotational equivalent is the angular impulse . Any time you give an object a spin, you are imparting an angular impulse to the object through the torque you apply. This in turn causes the system's angular moment to change. Equivalent to is

• The first relationship is not always true if the system is not a rigid body. Even for rigid bodies it may not be true if they are not rotating about a fixed axis. However, the second and third forms are always true even for a system of independent particles.

Rotational Equilibrium:
When an object is in equilibrium, it is not moving or rotating. The object's linear and angular accelerations are both zero.
* The sum of all the torques acting on a system must be equal to zero.
* The sum of the clockwise torques must be equal to the sum of the counterclockwise torques.
* The pivotal axis can be chosen to be any point inside or outside the object.
* It useful to observe that choosing the pivot point through the line of action of a force eliminates that force from the equilibrium torque equations. This often simplifies things.

 

Linear Static Equilibrium of the Center of Mass:
* The vector sum of all the forces acting on the object must be equal to zero.

* The sum of the horizontal components of all the forces must be equal to zero, and the sum of the vertical components of all the forces must be equal to zero.

* The sum of the components of the forces to the right must be equal to the sum of the components of the forces to the left, and the sum of the components of the forces up must be equal to the sum of the components of the forces down.

 

 

Torque Due to the Weight of an Object:
* The torque on a solid body (about any axis) produced by the object's own weight can be calculated as if all the object's mass were located at the center of mass of the object. Here the lever arm is the distance between the pivot point and the center of mass.
* Since freely rotating systems revolve about their center of mass, the weight of an object cannot create any torque on the object when it is rotating freely.

 

Rotational Equilibrium Problem-Solving
* Choose one object that is in equilibrium to be the system.

* Draw the free-body force diagram for this system. You will need this to calculate the torque for each force since the torque is the product of a force perpendicular to the lever arm times the lever arm distance to the pivot point.

* Choose a pivot point for the axis of rotation. You will need this to determine the lever arm of each force acting on the system.
Since the object does not rotate any point can be the chosen. However, some pivot points make the problem simpler to solve. In particular, choosing the pivot point to be along the line of action of some unknown force will eliminate that force.

* Choose a rotational direction to represent positive rotations. This is arbitrary but need to figure out what sign to put in front of each torque (or to determine which torques are CW and which are CCW). Having the wrong sign on some torque term is one of the most common sources of error.

* Pick at coordinate system so that you can resolve the static force vectors into components. Typically, they might be horizontal and vertical directions.

* Write down the static equilibrium conditions for your choice of coordinate systems.

or

* Write down the rotational equilibrium conditions.

or
S t = 0

* If all goes well, you should be able to solve the resulting expressions for any unknowns.

Man on a Plank Problem

A man who weighs 50.0 N stands 3.00 m from the right end of a board that is supported by two vertical cords attached to either end of the board. The board is 5.00 m long and weighs 10.0 N.
(A)	What is the tension in each of the two cords ?
(B)	What did the falling physicist say before he hit the ground ?

Sketch and Process:
.
A man stands on a plank suspended by two cords.

Frame of Reference:
There are several choices for the origin or pivot point: the left end of the plank, the right end of the plank, the location of the man, or the center of mass of the plank. All will give the same final results.
The location for the pivot point that is the simplest to solve is either end of the plank. If you place the origin at either of these two points, it eliminates one of the two unknown tensions since the torque created by the tension passing through that point is zero. We choose the right end of the plank.
We choose clockwise as the positive direction for the angular quantities.

Relevant Physics:
The system of the plank is in rotational and static equilibrium. The fundamental equations are:

Your major task is to figure out how to express these two principles in terms of the forces and torques acting on the plank. There are a total of four forces acting on the plank: the two tensions in the supporting cords, the weight of the man, and the weight of the plank itself.
The free-body force diagram for the plank looks like:

The Static Equilibrium Equation implies

Because this equation has two unknowns we cannot solve this problem using static equilibrium alone. We must also use rotational equilibrium to supply another condition.
Since the torque created by each force is equal to the force times its distance from the pivot point, the net torque on the board about its right end is given by,

Observe that the torque created by the weight of the plank itself can be found by assuming that the weight of the plank is located at the center of mass of the plank. Since it is assumed that the plank is uniform, this will be at the center of the plank.
The sign in front of each torque is determined by considering which way that torque would cause the plank to rotate about its right end. Positive is for CW (clockwise) rotations and negative is for CCW (counterclockwise) rotations, since we chose CW as the positive direction for rotations.
Also observe that if the two cords were not vertical then we would have to use Fnet,x = 0 to generate yet another condition. Moreover, the forces in the above equation for the tensions would be vertical components and not the total magnitude of the tension in non-vertical cords.
(A) Find the tension in each of the cords, T1 and T2.
Applying the equations for rotational and static equilibrium to the plank rotated about its right end we get,

Solving the rotational equilibrium equation for T1,

We can use the static equilibrium equation to find T2 since we now know T1.

Instead of using the static equilibrium equation, you could find T2 by switching the pivot point to the left end of the plank. The torque equation becomes,

Here the signs on the torque terms have changed, since the torques would cause the plank to rotate in the opposite direction if it was pivoted about its left end rather than its right end. Solving for T2,

This is the same result as before. This problem is unusual in that you can bypass using the static equilibrium equation altogether. In more complex problems, you will not only need to use the static equations (one for vertical and one for horizontal) but also switch pivot points to generate enough equations.

 

 

Alternate Solution using the Center of Mass as the Pivot Point:
The vertical static equilibrium equation is still the same. What changes is the torque equation since the pivot point is now located at the center of the board, i.e. this changes the length of the lever arms.

Note that the sign on the torque due to T2 is now negative, because by itself it would cause the plank to rotate CCW about its center of mass. The torque due to the man will still cause the plank to rotate CCW about the center of mass.
We have two linear equations with two unknowns which we could solve by a variety of methods. Simple substitution will work. Solve for T2 in the static equation and substitute it into the rotational equilibrium equation and solve for T1.

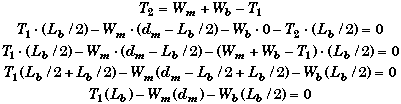
This last equation is the same equation we found when we chose the right end as the origin. This location of the origin will work, but there is more involved in solving the problem because this choice does not eliminate either of the unknowns. Had you been given the tension in the cords and asked to find the weight of the man and the plank, then this would be a good method to use.
b) Its not the fall that kills you, it is the large deceleration when you stop.

 

Two Torques on a Disk Problem

A solid horizontal disk with a mass of 3.00 kg and radius of 75.0 cm rotates on a frictionless bearing at its center. Two horizontal forces are applied to the disk at different locations with different angles. Force F1 is 15.0 N and is applied at an angle of 36.00 relative to due east. F1 is applied to a point that is 28.0 cm directly north of the disk's center. Force F2 is 22.0 N applied due east. F2 is applied to a point that is 63.0 cm from the disk's center and is 16.00 east of due south.
(A)	What is the net torque on the disk initially ?
(B)	What is the initial angular acceleration of the of the disk ?
(C)	What is the magnitude of a third force F3, applied tangentially to the rim of the disk -- needed to keep the disk from rotating ?

 

 

Sketch and Process:

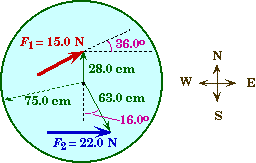
Two forces each exert a torque on disk that is free to rotate about its center.
(A) Find tnet.
Torque due to F1:
By itself, force F1 would cause the disk to rotate CW (clockwise), so its torque will be negative relative to the direction we chose as positive. The easiest way to handel this is to insert a negative sign in front of this torque's term to indicate that it is CW.
When calculating the torque we have three options.

Each equation gives the same results, so the question is "Which one is the simplest to apply?". To me it easiest to calculate the perpendicular component of force F1 since the angle of this force is given in the statement of the problem as 36.0o.

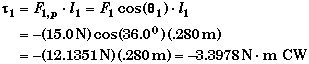
Equivalently, the angle between F1 and l1 is 900 - 360 = 540 so that

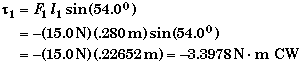
Finding the perpendicular lever arm is not so easy. We would need to draw another sketch to see how to determine the perpendicular lever arm from the information given. Whichever angle is used, the magnitude of the perpendicular lever arm is .22652 m.

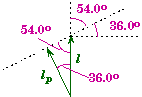
Torque due to F2:
Force F2will cause the disk to rotate CCW (counterclockwise) so its torque will be positive. To me it is easiest to calculate the perpendicular lever arm from the information given.

 

 

Total Torque:
The total torque is the sum of the two torques.

(B) Find the initial a.
To use Newton's Second Law for Rotation tnet = Ia we will need to calculate the disk's moment of inertia.

Solving tnet = Ia for a.

Since tnetis CCW, the disk's rotational acceleration will also be CCW.

• If the forces rotated with the disk, then the angular acceleration of the disk would remain constant. However if the forces' directions remained fixed, then the net torque would change as the disk rotated and the disk's angular acceleration would also change. In this case a would eventually become negative and the disk would oscillate back and forth.

(C) Find F3 such that a = 0.
If the disk does not rotate, then the net torque on the disk must be zero.

Since the torque is applied tangentially, its perpendicular lever arm will just be the radius of the disk. Using the definition of torque we get,

The negative sign means that the force will have to be applied in such a way that it creates a CW torque on the disk, and not that it is necessarily a negative force. If the force were applied to the top of the disk, it would have to be due east. On the other hand if it were applied to the bottom of the disk, it would have to be due west. If it were applied to the right hand side of the disk, it would have to be due south. You get the idea.

 

Which way will the Spool Roll

A 460 gram spool with an outer radius of 10.4 cm and inner radius of 5.00 cm has a cord wrapped around its inner hub with the cord emerging from the bottom part of the hub. The outer rim of the spool rest on a rough horizontal surface with a coefficient of kinetic friction equal to .330. The cord is pulled to the right by a force Fapp that is at an angle q to the horizontal.
(A)	There is a critical angle at which the cord can be pulled so that the spool does not rotate but slips to the right at a constant speed. Determine this critical angle.
(B)	What is the magnitude of the force applied at the critical angle if the spool is dragged to the right at a constant speed ?
(C)	Show that if the angle of the applied force is greater than the critical angle the spool will rotate clockwise and move to the left. Conversely, show that if the angle of the applied force is less than the critical angle the spool will rotate counterclockwise and move to the right.

Sketch and Process:

A spool is pulled by a force applied to its inner hub. Depending upon the angle at which the force is applied the spool will rotate either to the left or the right.
Relevant Physics:
The spool must obey Newton's second law for both its rotational motion and its horizontal linear motion.

The acceleration in vertical direction will always be zero since it is implied that the spool does not break contact with the surface.

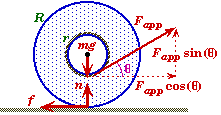
Sketching a free body force diagram will help determine what forces are acting on the spool and which of these forces will cause it to rotate. Only the applied force Fapp and the force of friction f can cause the spool to rotate about its center. Both the spool's weight and the normal force pass through the axis of rotation and can not produce any torque.
Vertical Direction:

Horizontal Direction:

Rotation Motion:
Since Fapp is always applied tangentially to the inner hub (no matter what the angle q) its perpendicular component is just its magnitude and its lever arm is radius of inner hub r. Likewise, the frictional force f is also acting tangentially and its lever arm is the radius of the outer rim R. The force of friction is opposite to the direction the edge of the spool would slip if there were no friction.

(A) Determine qc such that tnet = 0 and ax = 0.
When the spool is dragged at a constant speed so that is does not rotate, then both its horizontal acceleration and angular acceleration will be zero.
Horizontal Motion:

This means that the magnitude of the force of static friction will always be equal to the horizontal component of the applied force when the spool moves at a constant speed.
Rotational Motion:
The net torque on the spool is due the applied force and the static frictional force. Both forces are applied perpendicular to their lever arms..

Combining the two results

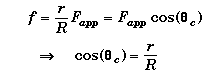
This is a surprisingly simple result. It means that the angle does not depend upon the mass of the spool, the coefficient of friction, or even the magnitude of the applied force but only upon the ratio of inner and outer radius.

(B) Find Fapp when q = qc and ax = 0 and the spool does not slip.
The maximum force that can be applied to the cord and not have the spool slip will occur when the static friction is at its maximum value f= fmax = µk n. We found the normal force in the relevant physics section.

Solving for Fapp,


(C) Determine which direction the spool will rotate if q > qc and q < qc.
To make life simple we assume that when q is not equal to qc, we pull the spool in such a way that its horizontal speed is constant. In this case we have seen that the frictional force must equal to the horizontal component of the applied force, .
Suppose the cord is horizontal, then f = Fapp. In this case the torque created by f will be greater than that created by Fapp since f's lever arm is longer. Thus it will rotate counterclockwise and move to the left. As Fapp is raised its torque remain the same. However, its horizontal component becomes smaller so the frictional torque becomes smaller. The two torques become equal at the critical angle. When q > qcthen the applied torque is larger and the spool will rotate to the right.

Let us prove this mathematically even when the spool's speed is not constant, which is the case if the spool starts from rest. We assume that the spool rotates without slipping while it is accelerating. This means the angular acceleration of the rim of the spool is related to its linear acceleration by .
The minus sign is necessary because we chose CCW as the positive direction. When the spool accelerates to the right it is rotating CW.
Horizontal Motion:

Rotational Motion:

Eliminating f and ax from these two equations.

Collecting terms and solving for a.

Thus when q < qc then a > 0 and the spool rotates CCW to the left. Similarly when q > qc then a < 0 and the spool rotates CW to the right.

 

 

Source : http://physics.mtsac.edu/4A/4A%20Text/Rotational%20Dynamics.doc

Web site link: http://physics.mtsac.edu/

Author : not indicated on the source document of the above text

If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.

 

Rotational dynamics

 

 

Rotational dynamics

 

Main page

 

Alimentation - nutrition	Animals	Architecture	Art
Astrology, esoteric, parapsychology and fantasy	Astronomy	Biology and genetics	Botany and agriculture
Chemistry	Courses, training, guides, handbooks and tips	Culture General and actuality	Dermatology, health and wellness
Dictionaries and glossaries	Economics and finance	Education and pediatrics	Engineering and technology
English grammar and anthology	Fashion and show business	Fitness	Food, recipes and drink
Games, play space	Geography, geology and environment	History	Informatics and computer world
Jobs world	Languages	Leisure and DIY do it yourself	Lessons for students
Literature, biographies and journalism	Mathematics, geometry and statistical	Medicine	Music
Notes and concept maps	Philosophy	Photography and images - pictures	Physics
Physiology	Psychology and psychoanalysis	Quiz questions and answers	Religions
Rights law and political science	Science	Sociology and cultural anthropology	Sport
Summaries and reviews	Television, film - movies and comics	Theater and communications	Theses, themes and dissertations
Travel and tourist guides	Useful documents and tables	Utility, calculators and converters	Weather and meteorology

 

 

This is the right place where find the answers to your questions like :

Who ? What ? When ? Where ? Why ? Which ? How ? What does Rotational dynamics mean ? Which is the meaning of Rotational dynamics?

 

---

 

---

 

 

 

Alanpedia.com from 1998 year by year new sites and innovations

Main page - Disclaimer - Contact us