Projectile motion
Projectile motion
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Projectile motion
A projectile is any object that falls through the air. These objects are accelerated downward by the force of gravity. They are also affected by their passage through the air, to varying degrees. We will ignore the effects of air resistance, however, which can be safely done if the object is dense and the distance that it falls is not too great.
 |
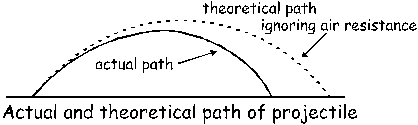Projectiles always follow a curved path called a trajectory (this trajectory is a segment of a parabola, a fact discovered by Galileo). Sometimes the trajectory is called a ballistic path. Such motion is three dimensional, but we will, for simplicity's sake, deal only with motion in two dimensions – up/ down, and sideways.
The key to efficiently deal with projectile motion is to simply break the velocity down into its horizontal and vertical components.
Vectors that are perpendicular to each other act independently. This is so important that the Physics Kahuna will rewrite it in large friendly letters to drive home its importance:
Vectors that are perpendicular to each other act independently.
This means that the horizontal and vertical components of a velocity vector don't affect each other. The up and down motion has nothing to do with the sideways motion and the sideways motion has no effect on the up and down motion.
This is like a really important KEY CONCEPT !
Assumptions:
We are required to make a couple of assumptions here:
- g has magnitude of 9.80 m/s2 and is always downward.
- Effect of air resistance can be ignored.
- Rotation of earth can be ignored.
- Motion (the horizontal velocity component) in the horizontal direction is constant.
The velocity of a projectile has two components, vx and vy.
vy = v sin q vx = v cos q
Note that we have already mastered the task of calculating these pesky components.
Projectile motion problems are quite simple – they require no really difficult mathematics nor do they really tax your brain. With stated, none-the-less, for some reason, students often struggle with them. Since you will not have a whole lot of time (we do got to move fast in the old AP world), you must take the time to master them.
The Physics Kahuna will help you. In this highly informative and user-friendly pub you will find in clear and concise prose all you need to know. So what do you need to know? Let’s find out.
Important concepts are:
horizontal velocity component is always constant
There is no acceleration in the horizontal direction.
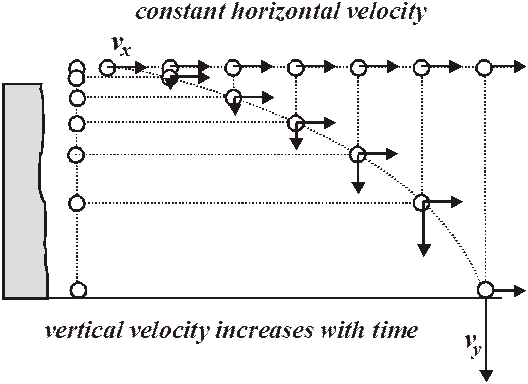
Recall the Physics Kahuna’s demonstration of the two bullet thing. The drawing above is a graphic depiction of the thing. The ball on the left simply falls – it has no horizontal motion. The other ball is launched with a horizontal velocity of vx. This horizontal velocity does not change and the ball moves sideways at a constant rate. They both fall downwards at exactly the same accelerating rate. They hit the ground at the same time. Do you see why this is so?
A projectile launched upwards at some angle would have a parabolic path that looks like the drawing below. Drawn on the projectile is its velocity vector and the x and y velocity components.
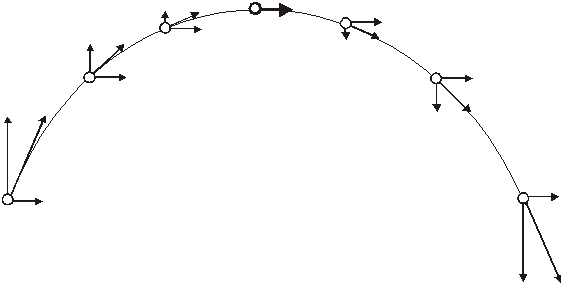
As long as the projectile is in the air, it will do two things:
It will move horizontally at a constant speed.
It will accelerate downwards at a constant rate of g.
The way you solve these problems is to break it into two problems, a constant motion horizontal motion problem and a vertical constant acceleration problem.
The best way to see how to do this is to jump in and solve some problems.
- A flagpole ornament falls off the top of a 25.0 m flagpole. How long would it take to hit the ground?
We assume that the ornament has no horizontal velocity. It falls straight down. We know how to do this problem.
so that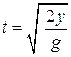 
Plug in the given values: 
- A stone is thrown horizontally from the top of a cliff that is 44.0 m high. It has a horizontal velocity of 15.0 m/s. We want to find how long it takes the stone to fall to the deck and how far it will travel from the base of the cliff.
This is like the flagpole problem, except that the stone has an initial horizontal velocity. But we know that the time it takes to hit the ground is the same as if it were falling straight down. (This is the key concept!!!). So finding the time is exactly like the previous problem. Once we’ve found the time, we can then find how far it travels horizontally.
Now that we know how long it takes to fall, we can figure out the horizontal distance it travels before it hits the ground. It has a constant horizontal speed, and can travel sideways at this speed as long as it is in the air falling, so to find x we use its average velocity and the time:
- A B-17 (a World War II era multiengine bomber) is flying at 375 km/h. The bombs it drops travel a horizontal distance of 5 250 m. What was the altitude of the plane at the time they had the old "bombs away"?
We have to find the time for the bomb to travel a horizontal distance of 5 250 m:
First we convert the bomber’s speed to meters per second:
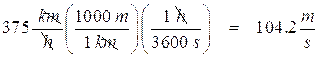
Then we can find the time it takes the bomb to travel a horizontal distance of 5 250 m.
Now we can find the vertical distance (altitude):
Upwardly Moving Projectiles:
One of the demonstrations that the Physics Kahuna is fond of is the hunter and the monkey demo. This is the one where the monkey is hanging from a tree in the jungle and the hunter wants to shoot it. Except that the monkey can instantly detect a gun shot and will let go of the branch and fall straight down. So where, was the main idea, should the hunter aim? Below the monkey, at the monkey, above the monkey?
Well we saw that the hunter should aim straight at the monkey. This is because the bullet will fall the same distance as the monkey, so when you aim at the monkey and fire the round, the monkey and the bullet will fall together and you will end up drilling the poor innocent little critter.
Physics can really be cruel, can’t it?
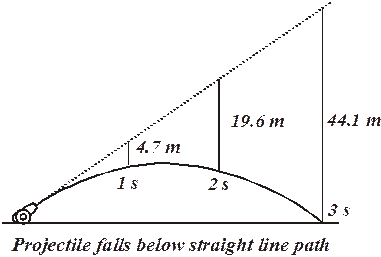
Here is the path of a projectile that is launched at some angle to the horizon. It has a horizontal velocity component and a vertical velocity component. For as long as it is in the air, it will be moving horizontally at vx. It will move upward because of its initial vertical velocity, vy. Gravity will act on it however, slowing it down. Eventually, at the top of the path, its vertical velocity will be zero. It will still have its horizontal velocity component, however. Then it will begin to fall downwards. When it finally reaches the same height it began with, its vertical speed will be the same as what it began with, but the direction of its velocity will be downwards instead of upwards (as it was at the beginning).
The projectile will travel a horizontal distance of x (this is often called the range). It will travel upwards a vertical distance of y. In half the total time of flight it will reach y and its vertical velocity will be zero.
There’s a lot of symmetry going on here.
We also assume that the projectile begins and ends at the same height. If this is not true, it will be spelled out in the problem.
- A ball is given an initial velocity of 22. 7 m/s at an angle of 66.0° to the horizontal. Find how high the ball will go.
To solve this problem, we have to find the vertical velocity of the ball. Once we know it, we can find how high it goes.
The ball starts out with vy and rises till its vertical velocity is zero. We can use these as the initial and final velocity of the ball.
Note that we have to pay attention here to the sign of the motion. We have both down and up motion and have to be clear about which direction is possible. Of course if the motion is in only one direction, we don’t have to worry about it.
- A naval gun fires a projectile. The gun’s muzzle velocity (so speed of the bullet) is 345 m/s at an elevation of 32.0 °. What is the range of the shot?
First find the vertical velocity:
Now we can find the time: 
We know that 
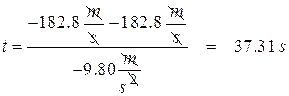
Now we can find the range since we know the time. First we find the horizontal velocity:
- A punter has a hang time of 4.5 s. If the ball travels down the field 48 m, what was the kick angle?
To find the angle of the kick, we need to use some trig. Probably the easiest thing to do would be to find the horizontal and vertical component of the velocity and use the tangent function to find the angle.
The horizontal speed is easy to find - we know the time and we know the range.
We can find the vertical velocity because we know the time that the ball is in the air – the time to go up and the time to go down.
Let’s look at the path for the ball from when it is at its max height to when it hits the ground. This means that its initial velocity is zero and its final velocity is vy.
The time for the ball to fall is half the total time.
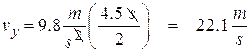
A stone is thrown off the top of a building from a height of 45.0 m. The stone has a launch angle of 62.5° and a speed of 31.5 m/s. (a) How long is the stone in flight, (b) how far from the base of the building does it travel? (c) What is its speed just before it hits the ground?
(a) First we find its vertical velocity component.
Now we can use this to find the time to reach its highest point.
Now we can find how high it rises:
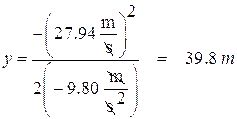
It took 2.85 s to reach this height, it will now fall this distance plus the height of the building before it hits the ground. So it will fall a distance of:
We can find the time to fall this distance:
The total time in the air is the total of these two times we found:
- We next find the distance from the base. This is easy since we know how long the projectile will be moving sideways:
First we find the horizontal velocity:
- To find the speed at the ground, we need to “recombine” the two components into the actual velocity vector. We can use the Pythagorean theorem for this:
Speed at ground: 
We need to find vy at the bottom. We know that the rock falls for a time of 4.16 s from its max height. We can use this to find its speed just before it hits.
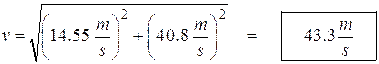
The first digital computer, called ENIAC (Electronic Numerical Integrator and Computer) became operational in 1946. It was funded by the Army in World War II. The purpose for the thing was to calculate trajectories for artillery shells to produce firing tables that the gun crews who served the guns could utilize. It could 500 numbers in only one second and could calculate the trajectory for a firing problem in only 30 seconds – a true miracle. It used electronic tubes and required 174 kilowatts of power (that’s 233 horsepower for you non-metric folks).
Anyway, the power needed to solve one trajectory problem was about the same as the amount of power generated by the powder charge during an actual fire mission for a single shell. Interesting.
Here we go, one last problem:
- You throw a potato at an angle of 22.2 °. If the thing is in the air for 1.55 s, how far did it go, distance-wise?
In half the time it will travel to its maximum height. It will fall back down to the earth in the other half of the time, so we can look at half the path, say from when it has an initial velocity of vy to when it reaches the highest point of its path where its vertical velocity is zero.
Since we know the angle and the vertical velocity, we can find the horizontal velocity.
We can now find the distance it travels since we know the time and the velocity:
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Kinematics/4%20-%20projectile.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Projectile motion
Projectile motion
Projectile motion
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Projectile motion mean ? Which is the meaning of Projectile motion?
Projectile motion physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us