Magnetism
Magnetism
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Magnetism
Physics - Magnetism
We’re going to look at magnets for a bit. The Physics Kahuna is absolutely convinced that all of his advanced students no exactly what a magnet is. No mystery here, you have got to be familiar with magnets. First of all, magnets are cool. You’ve probably had a magnet or two in your young life. There’s something wonderful about the way they can defy gravity and exert forces on things over distance. The Physics Kahuna would be willing to bet several shekels that you did a magnet experiment or two in grade school. Typical kind of thing would be to try and discover what kind of materials are attracted to magnets; steel screw – yes, wooden toothpick – no, penny – no, quarter – no, washer – yes, paperclip – yes, and so on.
If your elementary teachers were really good, you did the experiment where you put a piece of paper over a magnet and then sprinkled iron filings all around the magnet. The filings line up and make very interesting patterns.
Perhaps you learned to make a compass from a needle.
It turns out that magnets and magnetism are extremely important in modern life. Electric motors, TV’s, computers, electric generators, locomotives, CD players, all depend upon . . . well, you get the idea.
The first person to write about and study magnets was Thales about 2600 years ago. This is the same guy who looked into static electricity with the amber, remember? Thales found that rocks from a town called Magnesia could attract bits of iron. He called the things, "ho mangetes lithos" which means "the Magnesian rock". This is how the magnet got its name, from good old Magnesia (don’t confuse magnets from magnesia with Milk of Magnesia, which is a laxative).
Here’s your basic important circumstance --- magnetism and electricity are very closely connected – they are the two sides of a single coin, electromagnetism. So it’s interesting that one dude, Thales, was the first to study both of these two phenomena.
Magnet Basics: Magnetism has a lot of similarities to electricity. Electricity involves two charges, positive and negative. Magnets have two poles, the north pole and south pole.
Fundamental rule for magnets:
Like poles repel, unlike poles attract.
All magnets have these two poles. If you cut a magnet in half, the two new, smaller magnets will each have two poles. If you cut these halves into two more pieces, each of the new magnets will also have two poles. And so on. You can never slice a magnet in half and get only one pole. One of the interesting questions that modern physicists play around with is whether a magnet with a single pole can exist. Such a thing (which has never been discovered) is known as a monopole. Win yourself one of them Nobel Prizes in Physics get you one of them old monopoles.
Magnets exert forces on other magnets. They also can interact with other materials. The important interaction is the way they act with materials classed as ferromagnetic. These materials are strongly attracted to magnets. Ferromagnetic materials include the following elements: iron, cobalt, nickel, gadolinium, and dysprosium. Materials made with these elements (or compounds of these elements) are not only attracted to magnets, they can be magnetized and turned into magnets themselves.
Diamagnetic materials are weakly repelled by magnets. Many common materials are diamagnetic: water, glass, copper, graphite, salt, lead, rubber, diamond, wood, and many plastics for example.
Paramagnetic materials are weakly attracted to magnets. Examples: aluminum, oxygen, sodium, platinum, and uranium.
Magnetic Fields: Just as electric charges are surrounded by an electric field, so too are magnets surrounded by a magnetic field. We can even draw lines of force around the magnet to show the direction of the field and its strength. These are called magnetic lines of force or sometimes you see them referred to as magnetic lines of flux.
Here are some characteristics of a magnetic field:
- The lines of flux travel through the magnet
- They leave the magnet at the north pole.
- They travel through the air in a curve.
- The lines enter the magnet at the south pole.
- A line tangent to any point on a line of flux shows the direction of the field – which is the direction of the force that would be exerted on a north pole.
- Where the lines are close together the field is the strongest.
- The direction of the field is NORTH to SOUTH. The arrows point away from the north pole and towards the south pole.
In the drawing below you can see some of the lines of force of a bar magnet. Three points are located on the lines of force and the corresponding forces that would be exerted at each point are shown. The force is always tangent to the line of force.
The direction of the field is shown by the direction of the arrows.
Below are some of the lines of force between two magnets. The drawing on the left show the lines of force when two opposite poles face one another. The drawing on the right show the lines of force for two unlike poles.
The symbol for the magnetic field is B. The most common unit for the magnetic field is the Tesla (T). Other units can be used as well such as the gauss (G) and the Weber (Wb).
A Tesla is a newton per meter× ampere: 
Magnetic & Electrostatic Forces:
There are many similarities between magnetic and electrostatic fields. There are also a few differences.
- Both obey an inverse square law (just like gravity does).
- They can both be attractive or repulsive.
The primary difference between them is that the electrostatic charge can be a point charge, but magnets must always have a north and south pole.
Forces and Fields: Place a charged up balloon in a magnetic field – nothing happens. Magnetic fields don’t affect stationary charges. But a moving charge, well, that’s a whole different thing. A moving charge traveling through a magnetic field will experience a FORCE. The force exerted will be perpendicular to the motion of the charge and perpendicular to the direction of the field. The result of the force is to cause a deflection of the charged particle. It gets pushed to the side.
The equation for the force exerted on a moving charge by a magnetic field is:
FB is the magnetic force, B is the magnetic field in Tesla’s, q is the charge, v is the velocity of the charged particle, and q is the angle between the velocity direction and the direction of the magnetic field.
You will have this equation available for your use on the dreaded AP Physics Test.
The force on the charged particle is at a maximum when the velocity is perpendicular to the magnetic field. Note that if the velocity is in the direction of the magnetic field, the magnetic force will be zero.
The force is always perpendicular to the velocity and the magnetic field, B. This is shown in the drawing below. At the center is a particle that has a charge q. The direction of the magnetic field B is to the right. The particle’s direction is out of the sheet yer a lookin’ at. This is v. Therefore the force must be directed up.
To quickly figure out the direction of the force acting on the charged particle we can use the right hand rule.
Here’s how you use the rule. You take your right hand and keep it flat. Point your fingers in the direction of the magnetic field. (Fingers point to the south pole.) Point the thumb in the direction of the velocity of a positively charged particle. When your hand is contorted into this position, your palm will point in the direction of the force that will be acting on the charged particle.
The maximum force, FMax, occurs when the sine of the angle is one (which occurs when q = 90°),
The right hand rule gives the direction for the force acting on a particle that has a positive charge. If the charge on the particle is negative, then the direction of the force will be in the opposite direction. Or you could use your left hand in the same way.
Time to do a problem or two.
- A proton with a velocity of 6.8 x 106 m/s zooms through the earth’s magnetic field. (55 mT). What is the max magnetic force acting on the proton?
- A proton moving at 5.5 x 107 m/s along the x - axis enters an area where the magnetic field is 3.5 T directed at an angle of 45° to the x - axis lying in the xy plane. (a) What is magnitude of force? (b) What is direction of force? (c) What is the acceleration acting on the proton?
(a) The force is given by: 
(b) Using the right hand rule: Force is in the z direction.
- To find the acceleration we use the second law:
Magnetic Force and Work: For work to be done, a force has to act on an object, making it move. It would seem that a magnetic field could do work on a moving charged particle since it does exert a force on it. The other thing to remember, however, is that the force and the displacement have to be in the same direction.
We wrote this as: 
The cosine of a ninety degree angle is zero. So for the magnetic force, the work will be zero since the angle between the force and the motion is 90°.
A magnetic field does no work on a moving charged particle.
The force is always perpendicular to the magnetic field and the velocity. Therefore the force has no component in the direction of motion. Because of this, the magnetic force does no work
The force can only change the direction of the charge’s motion. It cannot change the kinetic energy of the particle. As the Physics Kahuna has previously stated, magnetic fields can only cause a deflection of the path of a moving charged particle.
Also please to remember that no force would be exerted on a charged particle that was at rest with respect to a magnetic field.
Motion of Charged Particle in Magnetic Field: Time to talk about some common conventions used to draw magnetic fields.
If we want to depict a magnetic field that is perpendicular to the sheet of paper that we have drawn the thing on, we can do this in two ways. If the direction of the magnetic field is out of the paper, then we represent the lines of force as little dots. (sometimes with a circle drawn around them). To show a uniform magnetic field, the dots are shown with equal spacing to the adjacent ones.
To show a magnetic field going into the paper, we represent the lines of force with an “”X”. Think of the “X” as being the tail of the vector. A dot is used to represent the head of the vector, indicating that the lines of force are coming out of the paper.
What happens when a charged particle moving at a constant velocity enters a uniform magnetic field? Well, outside of the field the particle will travel in a straight line – Newton’s first law, you know, objects in motion stay in motion unless acted upon by an outside force. Once the particle enters the field, an outside force does act on it. The magnetic field will exert a force on the particle.
The magnetic force will change the direction of the particle’s motion. The magnetic force will act on the charged particle all the time and will constantly change its direction as long as it is within the field.
This constant force acting to change the direction of the particle acts as a centripetal force.
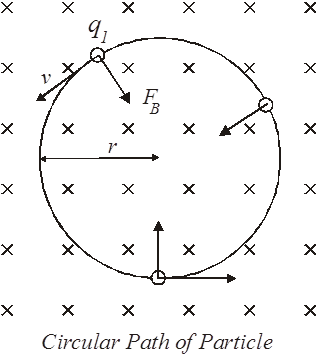
Can we figure out the radius of the curved path the particle will follow?
Yeah, you betcha! In fact, you must be prepared to derive an equation for the radius of the circular path using the second law, the equation for centripetal acceleration, and the magnetic force. You will have all three of these equations available to you.
Here’s what we do: The particle undergoes a centripetal acceleration. The equation for centripetal acceleration is:
This baby is provided on the test, right?
Using the second law, we can find the magnitude for the centripetal force.
Plug the centripetal acceleration into the second law:
The centripetal force is provided by the magnetic force exerted on the particle. The magnetic force is given by:
Here the angle q is 90 degrees so the sine is 1. Therefore:
Now we can set the centripetal force and the magnetic force equal to each other.
Solve this equation for the radius:
- A proton moves in a circular orbit of radius 15.0 cm in a uniform magnetic field of 0.500 T. If v is perpendicular to the field, find the speed of the proton.
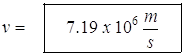
Note, examining the equation, one finds that the radius of the path is proportional to the momentum of the particle.
The momentum is, of course, mv.
The units get pretty hairy – how did the Physics Kahuna get m/s out of meters, Coulombs, Teslas divided by kilograms? Well, he just did. What is being said here is to not worry about it. Use standard units and they will all work out, like we did with electricity.
If the initial direction of particle’s velocity is not perpendicular to the magnetic field, then there will be an angle q between the field and the velocity. The path will end up being a type of spiral called a helix. This would be the general path of a charged particle in a magnetic field. The circular path is a special case that occurs only when the direction of the particle’s velocity is perpendicular to the field.
A proton in an electric field will experience a force that is parallel to the lines of force. This is shown in the drawing below on the left. Two plates are oppositely charged. A proton traveling perpendicular to the field enters the area between the plates. The proton is deflected towards the negative plate. You can see the plane that the path the proton takes.
The next drawing, the one on the right, shows the path a proton would take in a magnetic field. The proton’s initial velocity is perpendicular to the magnetic lines of force. The proton follows a circular path and is deflected at a right angle to the field and the velocity. The handsome drawing shows you the path and the plane it lies within.
A particle with an unknown mass and charge moves with a constant speed of v = 2.2 x 106 m/s as it passes undeflected through a pair of parallel plates as shown. The plates are separated by a distance of d = 5.0 x 10-3 m, and a constant potential difference V is maintained between them. A uniform magnetic field of B = 1.20 T directed into the page exists between the plates and to the right of them as shown. After the particle passes into the region to the right of the plates where only the magnetic field exists, it trajectory is circular with radius r = 0.10 m.
(a) What is the sign of the particle’s charge? Explain your answer.
(b) On the drawing, indicate the direction of the electric field provided by the plates.
(c) Determine the magnitude of the potential difference between the plates.
(d) Determine the ratio of charge to mass (q/m) of the particle.
- If the particle is positive, the magnetic force would be up and particle would curve above the plates. Since it goes the other way, it must have negative charge. Between the plates, the negative particle is deflected downwards. Therefore the electric field must force the negative particle up. The direction of the field is the direction a positive test charge would go so the field must be down. This way the particle will be deflected upward by the electric field of the plates.
(b)
- Finding the potential difference between the plates:
The electric field is given by 
The magnetic force from the magnetic field is: 
The electric force from the plates is: 
Set the two forces equal: 
plug in 
for E: 
- Finding the ratio of charge to mass:
From the circular path of the particle in the magnetic field, we know that:
The centripetal force = the magnetic force in the field
Set these two things equal to each other:
Solving for q/m (the charge to mass ratio):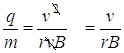 
Path in an Electric/Magnetic Field: What do we need for a charged particle to move with a constant velocity through a crossed electric and magnetic field (i.e., we have both a magnetic and electric field in the same space)?
In an electric field the particle will be deflected along the lines of force. In a magnetic field the particle will be deflected perpendicular to the lines of force. To get the particle to have a constant velocity, the magnetic force needs to cancel out the electric force, so they must be in opposite directions. This means that the magnetic field and the electric field have to be perpendicular to each other.
Earth as a Magnet: The earth has a magnetic field of its own. You can imagine the earth as having an enormous bar magnet stuck down the middle with one end sticking up out of the north pole and the other end sticking out of the south pole.
Please observe the lovely drawing to the right. You can see a sphere representing the earth with a bar magnet stuck through it. You will note that the south pole of the magnet is sticking up where we would normally expect to see the north pole.
This is because the north pole of a compass points to the geographic north. This means that the earth’s uppermost magnetic pole must be the south pole. All of which is very confusing.
We get around this by calling the end of the compass that point north the “north seeking pole”.
The compass is a small magnet that is free to rotate. When placed in the earth’s magnetic field the needle lines itself up with the lines of force -- it points north.
Lines of flux, as can be seen in the drawing, penetrate the surface of the earth. At the poles the lines of force are almost perpendicular to the earth’s surface. As you move towards the equator the angle gets smaller. This angle is called the dip angle. It varies with your location on the earth.
Magnetic Therapy Limited lists the following products: (All magnets and magnetic products are sold for experimental purposes only. They should not replace or substitute prescribed medical treatment.)
Magnetic Water Wand - Magnetic water in minutes... NEW
The Water Wand is a Magnetic Spindle, 1500 Gauss in strength with an 800 Gauss magnet which is encapsulated with a plastic coating in white.
It comes in Gold or Silver (Rhodium) Plated finish and is manufactured to a very high quality. The unique innovation is that the Water Wand is placed directly in the water or cold drink which means that it only then takes about 10 minutes to activate the water.
The Manufacturers, who are amongst the leaders in the field, explains that the Magnetic Water Wand also "Ionizes and Activates for a better taste and health".
Retail Price: £14.95
Our Price: £11.95
2500-Gauss MagDots
Our favorite product! We use these everywhere for up to 2-3 days of constant relief! Simply peel & stick to sore areas or acupressure points!
2500-gauss MagDots are (10) gold-plated neodymium magnets 30 adhesive patches.
Reg. $24.95
Now over 25% Off at $19.95!
The History Of Magnetic Therapy
Magnetic therapy dates back to 800 B.C. when physicians in ancient Greece, Egypt, and China practiced it. It was described in the books of Homer, Hippocrates, and Aristotle.
This ancient knowledge is now rediscovered, as people all over the world are searching for natural alternatives from modern medicine for healthy, energetic lives.
Magnetic therapy is accepted and widely used in Germany, Italy, England, France, Spain, Australia, and Russia.
"It is important to bring magnet therapy to the awareness of the interest lay public-particularly to those seeking help naturally."
Prof. Holger Hannemann, M.Sc Switzerland, 1990
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Electromagnetism/1%20-%20Magnet.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Magnetism
Magnetism
Magnetism
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Magnetism mean ? Which is the meaning of Magnetism?
Magnetism physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us