Dynamics of simple harmonic motion
Dynamics of simple harmonic motion
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Dynamics of simple harmonic motion
Dynamics of Simple Harmonic Motion
* Many systems that are in stable equilibrium will oscillate with simple harmonic motion when displaced by from equilibrium by a small amount.
 * Near equilibrium the force acting to restore the system can be approximated by the Hooke's law no matter how complex the "actual" force. For example, the force holding atoms together in a solid can be approximated by spring forces when the vibrations of atoms in a solid are small.
* Near equilibrium the force acting to restore the system can be approximated by the Hooke's law no matter how complex the "actual" force. For example, the force holding atoms together in a solid can be approximated by spring forces when the vibrations of atoms in a solid are small.
* For a one-dimensional system to undergo Simple Harmonic Motion, the equation of motion of the "Force Law" - Newton's Second Law - must take the form,
![]()
* This is a second order differential equation where
q(t) |
= Any spacial or angular coordinate of a system such as x or q |
K |
= Constant which is a function of system parameters |
* Any time you can reduce the "Force Law" equation to the above structural form, you know that the system will undergo Simple Harmonic Motion whose General Solution will look very similar to that of a mass-on-a-spring.
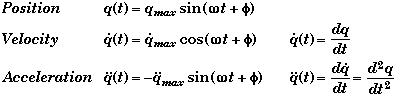

![]()
* One must examine the initial conditions to determine the actual value of the phase angle f since most calculator only returns values between ±p/2..
Hookes Law - Spring Force

Fs |
= Force exerted by the spring. SI: N |
k |
= Spring Constant. SI: N/m |
x |
= Displacement from equilibrium position. SI: m |
* The negative sign indicates that the spring force is a restoring force, i.e., the force Fs always acts in the opposite direction from the direction in which the system is displaced. Here we assume that the positive direction for values of x are the same as the positive values of the force.
* The origin has to be placed at the position where the spring system would be in static equilibrium for the equation Fs = -k x to be valid. This is the location were the net force on the object to which the spring is attached is equal to zero. If not, then Fs = -k(x - xo) where xo is equilibrium position relative to the origin.
* Springs are normally assumed to be massless so their inertia can be neglected. This also means that the force exerted by both ends of the spring are the same but in opposite directions.
MASS ON A SPRING - GENERAL SOLUTION
System: Mass attached to a horizontal spring resting on a horizontal, frictionless surface.
Newton's Second Law

Second Order Differential Equation
![]()
Solution as Function of Time
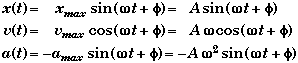
A |
= Amplitude (Considered to be a positive Constant) |
|
xmax |
= ± A |
Maximum position from equilibrium |
vmax |
= ± Aw |
Maximum velocity |
amax |
= ± Aw2 |
Maximum acceleration |
f |
= Phase Angle (SI: rad) |
|
w t + f |
= Circular motion rotational angle for SHM (SI: rad/s) |
|
|
Angular Frequency of Oscillation (SI: rad/s) |
|
|
(±p is determined by initial conditions) |
|
Period of one Complete Oscillation (SI: sec) |
||
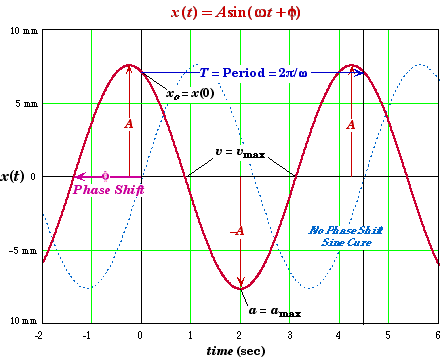
Conservation of Energy

Relationships Table
Example for a block is pulled to the right and released from rest.

* Except for time of occurrence, the relationships between maximum and minimum of the position, velocity, acceleration, kinetic energy, and potential energy are independent of the phase angle f, i.e. how the system is set into motion. For example, the velocity is always maximum when the acceleration is zero but this moment does not always occur at a quarter of the way through the period. However, the time between the events above are equal to 1/4 of the period. For example, the time between when the acceleration is at a maximum and when it is zero is 1/4 T.
Phase Angle
* The phase angle determines where in the cycle the motion starts, i.e. at what point in the cycle that t= 0.
At the start when time equal to zero, the initial conditions are:
![]()
These equations must be solved to find f.
Solution:
The two equations for the initial conditions can be combined into one equation.

This equation is the most useful when both xo and vo have non-zero values. The values in brackets are needed since your calculator only returns the principle value and not all possible values of the trigonometric inverse of the tangent function.
TWO EXAMPLES:
(1) System is at rest initially:
When the system is displaced and given no initial velocity, then the system starts out its initial position equal to its amplitude. In this case the phase angle has to be +p/2 or -p/2 since
![]()
If xo is also positive, then phase is +p/2 since
![]()
If xo is negative, then phase is -p/2.
(2) System is at the equilibrium position initially:
When the system is at the equilibrium position initially and given some initial velocity, then the system starts out with its maximum velocity. In this case the phase angle be either 0 or p since xo = A sin(f) = 0 when f = 0 or p. If the initial velocity of the system is positive then the phase angle is 0 whereas the phase angle is p if the initial velocity is negative. You can see that this is true since v(0) = vmax cos(0) = vmax > 0 , where as v(0) = vmax cos(p) -vmax < 0.
Third Law Problems:
Oscillating Beans Problem
The bottom of a vertical, massless spring is 88.0 cm above the floor. When a 660 gram can of beans is hung on the end of the spring and moved to equilibrium, the end of the spring is stretched until it is 76.0 cm above the floor. The beans are then lifted up from their equilibrium position until the top of the can is 80.0 cm above the floor and released. |
|
What is the spring constant of the spring ? |
|
Determine the equation of motion for the velocity of the can of beans as a function of time. |
|
At what height above the floor will the acceleration of the beans be equal to acceleration of gravity ? |
|
How fast are the beans moving exactly 3.80 seconds after theyx are released ? Are the beans above or below the equilibrium position ? |
|
How much work did it take to set the beans in motion ? |
|
How long does it take the beans to move from lowest position above the floor to their highest position above the floor ? |
|
What is the speed of the beans when they are 73.0 cm above the floor ?
|
|
Sketch and Process:

A can is hung on the end of a spring. After the weight has come to equilibrium, the can is set into harmonic motion by lifting the can and releasing it.
Frame of Reference:
There are three natural frames of reference:
- Level of the floor.
- Level of the unstretched spring.
- Level of the equilibrium position of the can when there is no motion.
The equations for simple harmonic motion are most easly expressed in a frame relative to the equilibrium position. We take downwards as the positive direction, since stretching a spring is taken as the positive direction in the generic equations for SHM.
The clock starts when the beans are released.
Relevant Physics:
A mass oscillating vertically on the end of a spring behaves like a horizontally oscillating mass with the equilibrium position shifted to the equilibrium position of the hanging mass. The force of gravity displaces the equilibrium position from the spring's unstretched position to the equilibrium position of the hanging mass, but otherwise the effects of gravity can be ignored.
To prove this we first apply Newton's Second Law to the can of beans, taking down as positive.
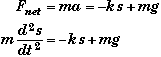
Here s is the displacement relative to the unstretched position of the spring which is 88.0 cm above the floor. When the beans are below 88.0 cm s is positive.
This equation does not look very much like the generic form of the differential equation of motion for SHM, which would be something like
![]()
We can transform the previous equation into the generic equation by observing that at equilibrium, the net force on the mass of the beans is zero.

Here so is the equilibrium position of the can relative to the unstreached spring. Replacing the downward force of gravity mg with kso we get
![]()
If we change to a new frame of reference centered around so such that x = s - so then
![]()
and the force equation has the same structure as the generic differential equation for SHM for the variable x.
![]()
Thus we can apply all the equations for SHM if we shift to a new variable x = s - so that is equal to zero when s = so.
The only equation we must modify is that of the mechanical energy. If we choose the equilibrium level to also be zero reference level for the gravitational potential, then PEg = -mgx since down is taken as positive direction, i.e. x is a negative number when the beans are above the equilibrium position so that -mgx will be positive when the beans are lifted. The total mechanical energy reduces to
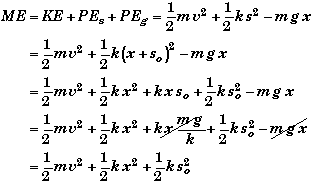
The amazing thing is that the gravitational potential energy cancels out when we change to this frame of reference. The mechanical energy is essentially just that of a simple harmonic oscillator plus the energy needed to stretch the spring to the equilibrium position (with the beans attached) from its unstretched position. This added term is constant and it will cancel out in the conservation of energy equations since it will appear on both sides of the equation.
(A) Find k, the spring constant.
At equilibrium, the force of the spring on the beans must be equal to the weight of the beans since the system is not moving. Applying Newton's 2nd Law to the system of the beans at equilibrium we can see that this is true.

(B) Find v(t).
The general form of the velocity equation for SHM is given by
![]()
Next we must determine the phase angle f. At t = 0
![]()
If we put this into the equation for position at time t = 0 we get,
![]()
Since x(0) = xo= -4.00 cm then f= -p/2. Recall that the can was lifted up initially and that down was taken as positive so that xo is a negative number initially. (The +p/2 would be the appropriate phase angle if we pulled the beans down by 4.00 cm initially.) Since A= 4.00 cm we see that the beans will oscillate ±4.00 cm around the equilibrium position or between 76.0 cm + 4.00 cm = 80.0 cm and 76.0 cm - 4.00 cm = 72.0 cm relative to the floor.
Finally we need to find the angular frequency w and vmax.
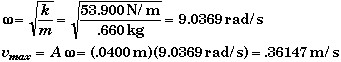
To three significant figures,
![]()
(C) Find height above the floor h when a = g.
Since we have chosen to place the origin at the equilibrium position, this means that we want to find the value of x such that x = 76 cm - h, when a = g. From SHM force equation, we know that the acceleration of any body undergoing SHM is equal to a = -(k/m)x. First find x and then h.

This means that as the beans oscillate, their acceleration will be equal to that of gravity when the end of the spring reaches its original unstretched length before the beans were attached to the spring. Since the A= 4.00 cm in this problem, the acceleration will never be equal to gravity, i.e. the beans must be lifted up (or pulled down) by more than 12.0 cm for the end of the spring to ever reach its unstretched position.
(D) Find v when t = 3.80 s.
In part (C) we found the general expression for the velocity as a function of time. Using this,

Since down is positive, this means the beans were moving down. There are two locations were the beans could have this same downward speed -- just after they were released or just before they stop at the bottom of their oscillation. To find out which, we need to determine the location of the beans at t = 3.80 s.
![]()
Thus the beans are near the bottom of their oscillation.
(E) Find work applied Wapp to lift the beans to xo.
There are two ways to find the work needed:
Using the Mechanical Energy of the oscillating system.
The work needed will be equal to the difference in mechanical energy between the beans' equilibrium position and its initial position.
![]()
Here the final state is what we have called the initial position when x = xo and vo= 0.

The initial state is the equilibrium position where x = 0 and v = 0.
![]()
Thus
![]()
Symbolically this would be
![]()
This is simply the work required to compress the spring from its equilibrium position.
Another way would be to calculate the work it would take to lift the beans a distance xo against gravity and then subtract the work done by the spring in contracting from so to so+ xo. Again recall that xo is a negative number so that so+ xo = 12.0 cm - 4.00 cm = 6.00 cm.

(F) How long will it take the beans to move from their lowest position to their highest position?
Since this is half the period of oscillation we want to find T/2 - half the period

(G) Find v when x = 76.0 cm -73.0 cm = 3.00 cm.
First note that there will be two solutions for the velocity. One solution when the beans are moving down, and another when the beans are moving up. It is obvious that these two solutions will have the same magnitude but be in opposite directions. If it is not obvious, we will show it when we find v.
There are two ways to find the speed. The simplest method is to use the conservation of energy. Another method is to use the general equation for velocity we found in part (B). However, we will also need to find the time when x= 3.00 cm to use the velocity equation.
Conservation of Energy Solution:
Assuming no energy is lost, the initial mechanical energy must equal the mechanical energy at any point.

Time solution:
Although more complicated, this method does show how to find the time given some location. To find the time we use the general equation for the position as a function of time and solve for the time when x = 3.00 cm.

There is another solution to the inverse sine function.
![]()
These correspond to the two times

The first is the time when the beans are moving down and the second when they are moving up. To find v we place these in
![]()
Note that we do not really need to put the time into this equation since we already know the values of wt- p/2 for the two times.
![]()
This is the same as before.
Block on Spring Problem
An 11.0 gram block attached to the right-end of a horizontal spring (on a frictionless surface) undergoes simple harmonic motion. The equation of motion of the block relative to the spring’s equilibrium position is given by, |
|
(A) |
What is the initial position and velocity of the block relative to the spring’s unstretched position? |
(B) |
How long does it take the block to move from its initial position to a position where the spring is maximally compressed? |
(C) |
What is the maximum force that the spring exerts on the block? |
(D) |
How much work did it take to set the block in motion if the spring was initially unstretched?
|
Sketch and Process:
A block oscillates on a frictionless surface because of its connection with a spring.

Relevant Physics:
This problem should give you some hands-on experience with the simple harmonic motion of a block on a spring that has already been solved in general.

A |
= Amplitude (Considered to be a positive Constant) |
|
xmax |
= ± A |
Maximum position from equilibrium |
vmax |
= ± Aw |
Maximum velocity |
amax |
= ± Aw2 |
Maximum acceleration |
f |
= Phase Angle (SI: rad) |
|
w t + f |
= Rotation angle for SHM (SI: rad/s) |
|
|
Angular Frequency of Oscillation (SI: rad/s) |
|
|
(±p is determined by initial conditions) |
|
|
Period of one Complete Oscillation (SI: sec) |
|
(A) Find x o and v o.
The initial position and velocity occur when t = 0. Using the given equation of motion,

The negative sign means that the spring is compressed at the start.
There are two ways to find the initial velocity. Since the velocity is the derivative of position,
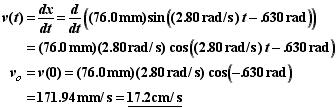
Alternately we could use the velocity equation for SHM,

The positive sign means the block is moving to the right initially. Thus the spring starts out compressed and is uncompressing after the block is given an initial velocity. This observation will be critical in part B.
(B) Find the time t B (measured from the start) for the spring to reach maximum compression.
At maximum compression x(t) = -A. Thus we need to solve the given equation of motion for the time when it is equal to -A.

When we take the trigonometric inverse we get two possible solutions,
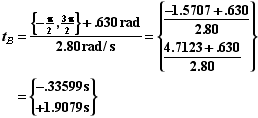
The positive solution is the correct answer.
![]()
The spring is also maximally compressed at -.336 seconds. If the initially velocity of the block had been to the left rather than the right then the answer would have been +.336 seconds. This would have happen if phase angle were positive rather negative.
An another way to see what is happing is to look at the period of oscillation,
![]()
From Part A we found that the spring starts off compressed and is uncompressing.
![]()
Thus the block has to move from its initial position out to where the spring is maximally stretched, return to its initial position, and then move to the point where the spring is maximally compressed. It is not surprising that the time t B would somewhat less than the period.
Yet another way to see what is happening is to plot the equation of motion function.
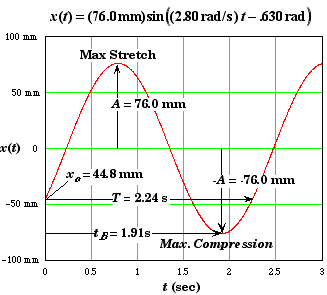
(C) Find F max.
Using Hooke’s Law for a mass on a spring,
![]()
From the SHM solution we know that,
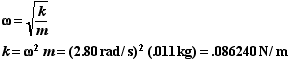
Thus,
![]()
Alternately, since we also know that a max = w2A for SHM, thus

This method is a little shorter since we did not have to find the spring constant first.
(D) Find the work to set the block into motion.
From the work-energy theorem we know that the work used to set the block into motion will equal to the change in mechanical energy of the block.
![]()
The initial mechanical energy is zero since the problem asks for the energy relative to the block equilibrium position where it has no velocity and the spring is unstreatched.
Since the mechanical energy is conserved we could find its value for any location of the block. Since we know the initial position and velocity from Part A,
![]()
We will need to find the spring constant k. From the SHM solution we know that,
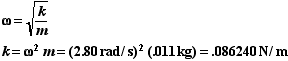
Thus,

However the mechanical energy can also be expressed in terms of either the maximum potential energy or the maximum potential energy.
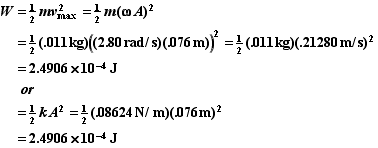
Circular Motion and the Phase Angle of SHM
The angle of rotation q(t) of a body undergoing uniform circular motion is related to the angle wt + f that appears in the sine and cosine functions in Simple Harmonic Motion. This is because circular motion viewed edge on is identical to simple harmonic motion.
Rotation Angle
 |
|
Phase Angle
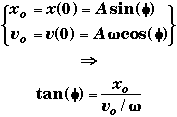 |
|
Simple Pendulum
A simple pendulum is modeled by a point mass attached to the end of a massless cord.

Since the motion of the mass is only in an arc, we can treat this problem as a rotational problem. The net (and only) torque acting on the mass is due to the component of the weight along the direction of the arc. (The tension in the cord cannot exert any torque on the bob since it acts through the center of rotation.)

This equation is not equivalent to the second order differential equation for SHM. However, when q is small (say less than 10o) then the value of sin(q) and q are nearly the same provided q is measured in radians.
![]()
This equation is structurally equivalent to the differential equation for SHM.
![]()
By matching terms we see that
![]()
and

Note that one has to distinguish between the angular frequency w of the SHM which is constant and the instantaneous angular velocity w' due to the rotational motion of a system which changes with time.
If the pendulum were pulled to the right and released then the phase angle would equal +p/2, the same as the simple mass on a spring example.
For small angles we have found that a simple pendulum should undergo SHM with a constant period T , that does not depend upon the mass or the amplitude of swing, but only upon the length of the cord and the acceleration of gravity. This is one of the reasons that pendulums have been used as clocks. On a grandfather clock, you can adjust the location of the mass to regulate the time kept by the clock.
Physical Pendulum
If a flat, rigid body is pivoted about any point other than its center of mass and displaced by a small angle, the body will execute SHM (Simple Harmonic Motion).

The derivation is similar to that of a simple pendulum since one can consider all the mass M to be located at the body's center of mass. Then a physical pendulum looks like a simple pendulum except that its moment of inertia is found using the parallel axis theorem.
![]()
Icm = the body's moment of inertia about its center of mass.
h = Distance from pivot point to the center of mass.
M = Mass of the body.
If the pivot joint is frictionless then the net torque acting on the planar object is given by the force of gravity perpendicular to lever arm, Mg sin(q), times the length of the lever arm, h:
![]()
When the angle of oscillation is small then the value of sin(q) and q or nearly the same provided q is measured in radians. Using this approximation, the above torque equation can be solved for the angular acceleration,
![]()
Since a =d2q/dt2, this equation is structurally similar to the differential equation for any type of SHM,
![]()
Matching terms with SHM equations,
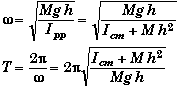
and
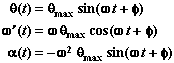
Here w' is instantaneous angular velocity of the body while w is angular frequency of the body's SHM. They are not the same. Moreover, w is constant while w' varies as the body oscillates back and forth.
Source : http://physics.mtsac.edu/4A/4A%20Text/Dynamics%20of%20Simple%20Harmonic%20Motion.doc
Web site link: http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Dynamics of simple harmonic motion
Dynamics of simple harmonic motion
Dynamics of simple harmonic motion
Springs calc
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Dynamics of simple harmonic motion mean ? Which is the meaning of Dynamics of simple harmonic motion?
Dynamics of simple harmonic motion physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us

