Acceleration
Acceleration
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Acceleration
Acceleration is the rate of change of velocity with respect to time*.
The unit of acceleration is the metre per second squared (m s-2, or m/s2 ).
Equations of Motion*
When an object (with initial velocity u) moves in a straight line with constant acceleration a, its displacement s from its starting point, and its final velocity v, change with time t.
Note that both v and u are instantaneous velocities.
The following equations tell us how these quantities are related:
v = u + at
s = ut + ½ at2
v2 = u2 + 2as
v = final velocity
u = initial velocity
a = acceleration
s= displacement (not distance)
t = time
Procedure for solving problems using equations of motion.
- Write down v, u, a, s and t underneath each other on the left hand side of the page, filling in the quantities you know, and put a question mark beside the quantity you are looking for.
- Write down the three equations of motion every time.
- Decide which of the three equations has only one unknown in it.
- Substitute in the known values in to this equation and solve to find the unknown.
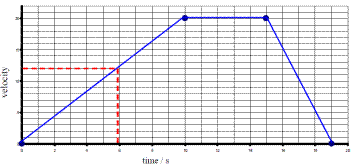
Velocity – Time graphs (for an object travelling with constant acceleration)
If a graph is drawn of Velocity (y-axis) against Time (x-axis), the slope of the graph is the acceleration of the object.
Acceleration due to Gravity: ‘g’
In the absence of air resistance, all objects near the Earth’s surface will fall with the same acceleration.
This acceleration is called acceleration due to gravity. Its symbol is ‘g’.
The value of g on the surface of the Earth is 9.8 ms-2.
We mention ‘on the surface of the earth’ because the value of g decreases as you move further away from the surface. We will see why when we study Gravitation.
We can now use this value when using equations of motion.
Notes
- Because we take the upward direction as positive, and because g is acting downwards, we take g to be minus (-) 9.8 m s-2 when answering maths questions (i.e. the initial velocity is usually opposite in direction to acceleration).
See problems 8, 9, 10 page 77. Then try questions 1 – 8, page 78.
- If an object is released from rest it means that initial velocity is 0 (u = 0).
- At the highest point of a trajectory, the (instantaneous) velocity is zero (object is not moving upwards or downwards).
- Also at the highest point of the trajectory, while the velocity is zero, the object is still accelerating at -9.8 m s-2.
See problem 10, page 77.
Derivation of the Three Equations of Motion
To Derive v = u + at
Þ v = u + at
To Derive s = ut + ½ at2
Vaverage = 
But v = u + at Þ Vaverage = 
Vaverage = 
Þ s = Vaverage(t) Þ s = 
(t)
Þ s = ut + ½ at2
To Derive v2 = u2 + 2as
v = u + at Þ v2 = u2 + 2uat + (at)2 {multiply out both sides}
We can rewrite this as v2 = u2 + 2a(ut + ½ at2) {because 2a(ut + ½ at2) = 2uat + (at)2}
Now sub in s = ut + ½ at2 Þ v2 = u2 + 2as
Mandatory Experiment
- To measure acceleration using a ticker tape timer
- To measure acceleration due to gravity using a Free-Fall Apparatus
See page 78
Before attempting this experiment you should answer Question 2, page 30 of the workbook.
You should also try to answer the questions on page 80 of the textbook
Leaving Cert Physics Syllabus: Acceleration
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Linear Motion |
Acceleration: definition and unit. |
Measurement of acceleration using any suitable apparatus. |
Sports, e.g. athletics. |
|
|
|
|
|
Equations of motion. |
Measurement of g. |
|
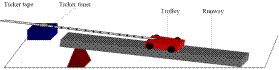
MEASUREMENT OF ACCELERATION
APPARATUS : Ticker timer and tape, a.c. power supply, trolley, runway
DIAGRAM
PROCEDURE
- Set up the apparatus as in the diagram.
- Connect the ticker timer to a suitable low-voltage power supply.
- Allow the trolley to roll down the runway.
- The trolley is accelerating as the distance between the spots is increasing.
- The time interval between two adjacent dots is 0.02 s, assuming the ticker timer marks fifty dots per second.
- Mark out five adjacent spaces near the beginning of the tape. Measure the length s1.
- The time t1 is 5 × 0.02 = 0.1 s.
- We can assume that the trolley was travelling at constant velocity for a small time interval.
Thus initial velocity u = distance/time = s1/t1
- Similarly mark out five adjacent spaces near the end of the tape and find the final velocity v.
- Measure the distance s in metres from the centre point of u to the centre point of v.
- The acceleration is found using the formula: v2 = u2 + 2as or a = v2 – u2 / 2s
- By changing the tilt of the runway different values of acceleration are obtained. Repeat a number of times.
- Tabulate results as shown.
RESULTS
s1 (m) |
t1(s) |
u (m s -1) |
s2 (m) |
t2(s) |
v (m s -1) |
s (m) |
a (m s-2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CONCLUSION
We set out to measure acceleration and at the end of the day that’s exactly what we did. We conclude with the ardent wish that not all experiments are this mind-numbingly boring.
NOTES
- Ignore the initial five or six dots on the tape since the trolley may not be moving with constant acceleration during this time interval.
- Ticker timers that use pre-carbonated tape are recommended because the friction due to paper drag is reduced.
- Ensure that the voltage rating of the timer is not exceeded.
- Some timers make one hundred dots in one second.
MEASUREMENT OF ACCELERATION DUE TO GRAVITY (g) USING THE FREEFALL METHOD
APPARATUS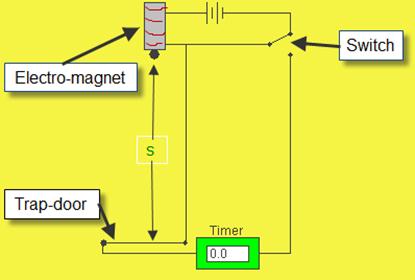 
: Millisecond timer, metal ball, trapdoor and electromagnet.
DIAGRAM
PROCEDURE
- Set up the apparatus as shown. The millisecond timer starts when the ball is released and stops when the ball hits the trapdoor.
- Measure the distance s using a metre stick.
- Flick the switch to release the ball and record the time t from the millisecond timer.
- Repeat for different values of s.
- Calculate the values for g using the equation s = (g/2) t2. Obtain an average value for g.
- Draw a graph of s against t2 and use the slope to find a value for g (g will be twice the slope).
RESULTS
s (m) |
|
|
|
|
|
|
|
|
t(s) |
|
|
|
|
|
|
|
|
t2 (s2) |
|
|
|
|
|
|
|
|
g (m s-2) |
|
|
|
|
|
|
|
|
gavg = |
||||||||
CONCLUSION
When we plotted the graph, the slope worked out to be 4.85, which resulted in a value for g of 9.9 m s-2, which is pretty damn close to the theoretical value of 9.8 m s-2. Conclusion? We rock!
PRECAUTIONS / SOURCES OF ERROR
- For each height s repeat three times and take the smallest time as the correct value for t.
- Place a piece of paper between the ball bearing and the electromagnet to ensure a quick release.
- Remember to convert from milliseconds to seconds.
NOTE
Both points 1 and 2 above are associated with the problem that even though you switch off the power for the electromagnet (and in so doing switch on the timer) it will not lose its magnetism immediately, therefore the ball will not fall straight away. This means that the reading on the timer will always be (slightly) longer than the time for which the ball was dropping.
Extra Credit
I was recently riding as a passenger in a van and there was a housefly buzzing around in the van. While trying to squash the fly, I was wondering why was the fly travelling at the same speed as the van at 70 mph as it was hovering in mid air. Shouldn't it have smashed into the rear window of the van just like so many bugs would have been, on the grill of the vehicle??
*Acceleration is the rate of change of velocity with respect to time.
Consider an object which is falling through the air. Its instantaneous velocity after one, two, three and four seconds is given in the following table:
Time |
Velocity |
1 second |
10 m/s |
2 seconds |
20 m/s |
3 seconds |
30 m/s |
4 seconds |
40 m/s |
We can see that with every second that passes the velocity increases by 10 m/s.
Alternative ways of writing this are that the velocity increases by 10 m/s per second or 10 m/s/s or 10 m/s2 or 10 m s-2.
*Equations of Motion puzzle
Take two of the above formulae: v = u + at and s = ut + ½ at2.
Assume a particle begins from rest so both formulae reduce to v = at and s = ½ at2.
Cross-multiply to get a on its own on both sides: a = v/t and a = 2s/t2.
Equate both right hand sides: v/t = 2s/t2.
Divide both sides by t: v = 2s/t.
Substitute v for s/t on the right hand side (because velocity equals distance divided by time) and you get v = 2v, or 1 = 2 !!
Hint: The mistake here is to do with the concept of instantaneous velocity.
Did you know?
The release of stored elastic strain energy often drives rapid movements (trebuchet, catapult, long and cross bows, jumping flea, froghopper insect, venus flytrap).
When a flea jumps, the rate of acceleration is 20 times that of the space shuttle during launch
The flower stamens of the american bunchberry dogwood rely on this principle to eject pollen as the flower opens explosively in less than 0.5 ms.
Analysis of hi-speed video images shows that the stamens maximum acceleration is typically 2400g
(i.e. ~ 24,000 m s-2), with a maximum speed of 3.1 m s-1. This speed is necessary to propel the pollen, as it is rapidly decelerated by air drag to its terminal speed of 0.12 m s-1.
Nevertheless the height reached by the pollen is typically 2.5 cm, which is ten times the height of the flower itself. At 2.5 cm the pollen can be carried away by the wind.
Why s for displacement?
Answer 1: It seems that we use s for displacement (with equations of motion) because they were devised by Galileo and he used the first letter from the Latin for distance, 'spatia'.
Answer 2: Pre 1900 s was used for "space covered" and velocity was "space covered" divided by time.
"Space covered" became distance. S was used until about 1940-50 when d became in fashion.
I have no idea why acceleration is assigned the letter f in the equations of motion given in the log tables.
The Jerk and the Jounce
So if the rate of change of position with respect to time is velocity, and the rate of change of velocity with respect to time is acceleration, what about the rate of change of acceleration with respect to time?
Apparently this is called the jerk, and before you ask, the next one is called the jounce (or maybe it’s the other way around). Either way, these are important considerations when one is building a roller-coaster or space shuttle. I have an Open University video of this (it may even be on YouTube by the time you read this. This may not be the most exciting concept in the world (unless you happen to be considering Engineering as a career, in which case you will find this positively orgasmic).
Or so I’m told.
Perhaps I shouldn’t be so dismissive. I imagine these may well be taken into consideration when designing action video-games.
Exam questions
- [2006][2002 OL][2004 OL][2008 OL][2009 OL]
Define velocity.
- [2002 OL][2004 OL][2008 OL]
Define acceleration.
- [2005 OL]
A car accelerates from 10 m s−1 to 30 m s−1 in 5 seconds. What is its acceleration?
- [2002 OL]
An aircraft was travelling at a speed of 60 m s-1 when it landed on a runway. It took two minutes to stop. Calculate the acceleration of the aircraft while coming to a stop.
- [2004 OL]
A cheetah can go from rest up to a velocity of 28 m s−1 in just 4 seconds and stay running at this velocity for a further 10 seconds.
- Sketch a velocity−time graph to show the variation of velocity with time for the cheetah during these 14 seconds.
- Calculate the acceleration of the cheetah during the first 4 seconds.
- [2008]
In a pole-vaulting competition an athlete, whose centre of gravity is 1.1 m above the ground, sprints from rest and reaches a maximum velocity of 9.2 ms–1 after 3.0 seconds. He maintains this velocity for 2.0 seconds before jumping.
- Draw a velocity-time graph to illustrate the athlete’s horizontal motion.
- Use your graph to calculate the distance travelled by the athlete before jumping.
- [2008 OL]
A speedboat starts from rest and reaches a velocity of 20 m s−1 in 10 seconds.
It continues at this velocity for a further 5 seconds.
The speedboat then comes to a stop in the next 4 seconds.
- Draw a velocity-time graph to show the variation of velocity of the boat during its journey.
- Use your graph to estimate the velocity of the speedboat after 6 seconds.
- Calculate the acceleration of the boat during the first 10 seconds.
- What was the distance travelled by the boat when it was moving at a constant velocity?
- [2007]
A car is travelling at a velocity of 25 m s-1 when the engine is then turned off; calculate how far the car will travel before coming to rest if the deceleration is 1.47 ms-2?
- [2009]
A skateboarder starts from rest at the top of a ramp and accelerates down it. The ramp is 25 m long and the skateboarder has a velocity of 12.2 m s–1 at the bottom of the ramp.
Calculate the average acceleration of the skateboarder on the ramp.
- [2010 OL]
A cyclist on a bike has a combined mass of 120 kg.
The cyclist starts from rest and by pedalling maintains an acceleration of the cyclist of 0.5 m s–2 along a horizontal road.
- Calculate the maximum velocity of the cyclist after 15 seconds.
- Calculate the distance travelled by the cyclist during the first 15 seconds.
- The cyclist stops peddling after 15 seconds and continues to freewheel for a further 80 m before coming to a stop.
Calculate the time taken for the cyclist to travel the final 80 m?
- [2009 OL]
A train started from a station and accelerated at 0.5 m s−2 to reach its top speed of 50 m s−1 and maintained this speed for 90 minutes.
As the train approached the next station the driver applied the brakes uniformly to bring the train to a stop in a distance of 500 m.
- Calculate how long it took the train to reach its top speed.
- Calculate how far it travelled at its top speed.
- Calculate the acceleration experienced by the train when the brakes were applied.
- [2010]
The graph shown represents the motion of a cyclist on a journey.
Using the graph, calculate the distance travelled by the cyclist and the average speed for the journey.
- [2003 OL][2006 OL]
What is meant by the term acceleration due to gravity?
- [2005]
A basketball which was resting on a hoop falls to the ground 3.05 m below.
What is the maximum velocity of the ball as it falls?
- [2006 OL]
An astronaut drops an object from a height of 1.6 m above the surface of the moon and the object takes 1.4 s to fall. Calculate the acceleration due to gravity on the surface of the moon.
- [2003 OL]
- An astronaut is on the surface of the moon, where the acceleration due to gravity is 1.6 m s–2.
The astronaut throws a stone straight up from the surface of the moon with an initial speed of 25 m s–1. Describe how the speed of the stone changes as it reaches its highest point.
- Calculate the highest point reached by the stone.
- Calculate how high the astronaut can throw the same stone with the same initial speed of 25 m s–1 when on the surface of the earth, where the acceleration due to gravity is 9.8 m s–2.
- [2003]
A skydiver falls from an aircraft that is flying horizontally. He reaches a constant speed of 50 m s–1 after falling through a height of 1500 m. Calculate the average vertical acceleration of the skydiver.
- [2006]
The student releases the ball when is it at A, which is 130 cm above the ground, and the ball travels vertically upwards at a velocity of 7 m s-1.
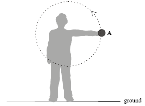Calculate the maximum height, above the ground, the ball will reach.
- [2006]
The student releases the ball when is it at A, which is 130 cm above the ground, and the ball travels vertically upwards at a velocity of 7 m s-1.
Calculate the time taken for the ball to hit the ground after its release from A.
Mandatory experiments
- [2004 OL]
Describe an experiment to measure the velocity of a moving object.
- [2008 OL]
A student carried out an experiment to find the acceleration of a moving trolley.
The student measured the velocity of the trolley at different times and plotted a graph which was then used to find its acceleration. The table shows the data recorded.
Velocity/ m s-1 |
0.9 |
1.7 |
2.5 |
3.3 |
4.1 |
4.9 |
Time/s |
0 |
2 |
4 |
6 |
8 |
10 |
- Describe, with the aid of a diagram, how the student measured the velocity of the trolley.
- Using the data in the table, draw a graph on graph paper of the trolley’s velocity against time. Put time on the horizontal axis (X-axis).
- Find the slope of your graph and hence determine the acceleration of the trolley.
- [2002 OL]
You have carried out an experiment to measure g, the acceleration due to gravity.
- Draw a labelled diagram of the apparatus you used.
- Describe the procedure involved in measuring the time in this experiment.
- As well as measuring time, what other measurement did you take?
- Outline how you got a value for g from your measurements.
- Name one precaution you took to get an accurate result.
- [2009 OL]
You carried out an experiment to measure g, the acceleration due to gravity.
- Draw a labelled diagram of the apparatus you used.
- State what measurements you took during the experiment.
- Describe how you took one of these measurements.
- How did you calculate the value of g from your measurements?
- Give one precaution that you took to get an accurate result.
- [2009]
s/ cm |
30 |
50 |
70 |
90 |
110 |
130 |
150 |
t/ms |
247 |
310 |
377 |
435 |
473 |
514 |
540 |
In an experiment to measure the acceleration due to gravity, the time t for an object to fall from rest through a distance s was measured. The procedure was repeated for a series of values of the distance s. The table shows the recorded data.
- Draw a labelled diagram of the apparatus used in the experiment.
- Indicate the distance s on your diagram.
- Describe how the time interval t was measured.
- Calculate a value for the acceleration due to gravity by drawing a suitable graph based on the recorded data.
- Give two ways of minimising the effect of air resistance in the experiment.
- [2004]
In an experiment to measure the acceleration due to gravity g by a free fall method, a student measured the time t for an object to fall from rest through a distance s.
This procedure was repeated for a series of values of the distance s.
The table shows the data recorded by the student.
s/cm |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
t/ms |
244 |
291 |
325 |
342 |
371 |
409 |
420 |
- Describe, with the aid of a diagram, how the student obtained the data.
- Calculate a value for g by drawing a suitable graph.
- Give two precautions that should be taken to ensure a more accurate result.
Exam solutions
- Velocity is the rate of change of displacement with respect to time.
- Acceleration is the rate of change of velocity with respect to time.
- v = u + at Þ a = ( v – u ) ÷ t Þ a = (30 – 10) ÷ 5 Þ a = 4 m s-2.
- v = u + at Þ 0 = 60 + a (120) Þ a = - 0.5 m s-2
- See diagram
- v = u + at Þ 28 = 0 + a (4) Þ a = 7 m s-2
- See diagram
- Distance (s) = area under curve
s = ½ (3)(9.2) + 2 (9.2) / 13.8 + 18.4 / 32.2 m
- 12 m s-1.
- v = u + at but u = 0 Þ a = v/t = 20/10 = 2 m s-2.
- v = s/t Þ s = vt = 20 × 5 = 100 m
- v 2 = u 2 + 2as
0 = 25 +2(-1.47) s or s = 213 m
- v2= u2 + 2as Þ (12.2)2 = 0 +2a(25)
a = 2.98 m s–2
- v = u + at.
v = u + (0.5)(15) = 7.5 m s–1
- s = ut + ½ at2
s = 0 + ½ (0.5)(15)2 = 56.25 m.
- s = (u +v)t/2
80 = (7.5 + 0)t/2
t = 21.33 s
- v = u + at
50 = 0 + 0.5t
t = 50/0.5 = 100 s
- s = ut + ½ at2 (but a = 0)
s = 50 × (90×60) = 270000 m
- v2 = u2 + 2as
0 = 502 + 2a(500)
a = −2500/1000 = − 2.5 m s-1
- Distance travelled = area under the graph
18 km h-1 = 18000/60 m s-1 = 300 m min-1
S1 = 150 × 6 = 900 m
S2 = 300 × 8 = 2400 m
S3 = 150 × 5 = 750 m
Total distance = 4050 m
Average speed = total distance divided by total time = 4050/19 = 213.2 m min-1 = 3.55 m s-1
- It is the acceleration of an object which is in freefall due to the attraction of the earth.
- v2 = u2 +2as Þ v2 = 0 + 2(9.8)(3.05) Þ v2 = 59.78
v = 7.73 m s-1
- s = 1.6 m, t = 1.4 s, u = 0. Substitute into the equation s = ut + ½ at2 to get a = 1.6 m s-2.
- It slows?
- v2 = u2 + 2as Þ 0 = (25)2 + 2 (-1.6) s Þ s = 195.3 m.
- v2 = u2 + 2as Þ 0 = (25)2 + 2 (-9.8) s Þ s = 31.9 m.
- v 2= u2+2as Þ 502 = 0 + (2)(a)(1500) Þ a = 0.83 m s-2
- v2 = u2+ 2as Þ 0 = (7)2 + 2(-9.8) s / s = 2.5(0) m Þ max. height = 2.5 + 1.30 / 3.8 m
- s = ut + ½ at2
-1.30 = 7t – ½ (9.8)t2
t = 1.59 s
Mandatory experiments
- We measured the distance between 11 dots on the tape.
- The time taken to cover that distance corresponded to the time for 10 intervals, where each interval was 1/50th of a second.
- We calculated velocity using the formula velocity = distance/time.
- He measured the distance between 11 dots on the tape.
The time taken to cover that distance corresponded to the time for 10 intervals, where each interval was 1/50th of a second. - He calculated velocity using the formula velocity = distance/time.
- See graph
Take any two points e.g. (0, 0.9) and (10, 4.9) and use the formula: slope = y2 – y1 / x2 – x1
Slope = acceleration = 0.4 m s-2
See diagram- When we flicked the switched it turned on the timer and this remained on until the ball fell through the trap-door at the bottom. The time was then read from the timer.
- The distance travelled by the ball.
- s = ut + ½ (g) t2 Þ g = 2s/t2
- For a given length repeat and use the smallest time value recorded for t.
See diagram- Distance s as shown on the diagram, time for the object to fall.
- Measure length from the bottom of the ball to the top of the trapdoor as shown using a metre stick.
The time is measured using the timer which switches on when the ball is released and stops when the ball hits the trap-door.
- Plot a graph of s against t2; the slope of the graph corresponds to g/2.
Alternatively substitute (for t and s) into the equation s = (g/2) t2
- Use the smallest time value recorded for t, repeat the experiment a number of times
- Timer, ball, release mechanism, trap door
- (Perpendicular) distance indicated between bottom of ball and top of trap door.
- Timer starts when ball leaves release mechanism
Timer stops when ball hits trap door.
s/ cm |
30 |
50 |
70 |
90 |
110 |
130 |
150 |
t/ms |
247 |
310 |
377 |
435 |
473 |
514 |
540 |
t 2 / s2 |
0.0610 |
0.0961 |
0.1421 |
0.1892 |
0.2237 |
0.2642 |
0.2916 |
- Axes correctly labelled
- points correctly plotted
- Straight line with a good distribution
- Correct slope method
- Slope = 5.02 // 0.198
- g = (10.04 ± 0.20) m s–2
- Small (object)/ smooth(object)/ no draughts/ in vacuum/ distances relatively short / heavy (object) / dense / spherical/ aerodynamic .
- [2004]
- The clock starts as sphere is released and stops when the sphere hits the trapdoor.
S is the distance from solenoid to trap-door.
Record distance s and the time t
s/cm |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
t/ms |
244 |
291 |
325 |
342 |
371 |
409 |
420 |
t2 /s2 |
0.060 |
0.085 |
0.106 |
0.117 |
0.138 |
0.167 |
0.176 |
- Calculation of t2(at least five correct values)
Axes s and t2 labelled
At least five points correctly plotted
Straight line with good fit
Method for slope
Correct substitution
g = 10.0 ± 0.2 m s−2
- Measure from bottom of sphere; avoid parallax error; for each value of s take several values for t / min t reference;); adjust ‘sensitivity’ of trap door; adjust ‘sensitivity’ of electromagnet (using paper between sphere and core); use large values for s (to reduce % error); use millisecond timer
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/7.%20Acceleration.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Acceleration
Acceleration
Acceleration
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Acceleration mean ? Which is the meaning of Acceleration?
Acceleration physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us