Gases
Gases
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Chemistry
Gases
- The three states of matter include solid, liquid and gas.
- The states of matter can be differentiated by the following:
State |
Characteristics |
Solids |
Definite shape and definite volume |
Liquids |
Varied shape and definite volume |
Gases |
Varied shape and varied volume |
Gases in the Atmosphere
- Gases in our atmosphere perform a major function in sustaining life on our planet. The atmosphere is needed for:
- breathing and cellular respiration
- C6H12O6(s) + 6 O2(g) ® 6 CO2(g) + 6 H2O(g)
- photosynthesis in plants
- 6 CO2(g) + 6 H2O(g) ® C6H12O6(s) + 6 O2(g)
- protection from harmful solar radiation such as ultraviolet light (UV rays)
- transmission of heat and water vapour throughout the earth
Composition of Gases in the Atmosphere
Gas |
Percentage By Volume |
nitrogen (N2(g)) |
78.1 |
oxygen (O2(g)) |
20.9 |
argon (Ar(g)) |
0.93 |
carbon dioxide (CO2(g)) |
0.03 |
neon (Ne(g)) |
0.002 |
helium (He(g)) |
0.0005 |
krypton (Kr(g)), xenon (Xe(g)), methane (CH4(g)), hydrogen (H2(g)) |
trace amounts |
nitrogen oxides (NO2(g), NO3(g)) |
trace amounts |
sulfur oxides (SO2(g), SO3(g)) |
trace amounts |
water vapour |
trace amounts |
- Although nitrogenand oxygen gases make up about 99 % of our atmosphere, other gases are a source of pollution. For example:
- SO2(g) and SO3(g) are called sulfur oxides and contribute to acid rain.
- SO2(g) + H2O(g) ® H2SO3(aq) sulfurous acid
- NO(g) and NO2(g) are called nitrogen oxides and contribute to acid rain.
- NO(g) + H2O(g) ® HNO2(aq) nitrous acid
- CO(g) is given off in incomplete hydrocarbon combustion reactions.
Properties of Gases
- Under normal conditions, over 99.9 % of the total volume of a gas is empty space, therefore gases can be easily compressed.
- Because gas particles or molecules move continuously in a straight line until they hit another object, they spontaneously fill the entire space available. This process can be termed diffusion.
- When gas particles collide, no energy is lost so their collisions are said to be elastic.
- The higher the temperature of a gas, the more kinetic energy it has and therefore the faster it can move.
Gas Pressure
- Pressure is defined as a force exerted on an area.
- A force is a push or pull and is measured in newtons (N).
- Area is measured in square metres (m2).

- When gas particles hit a wall or obstacle, they collectively exert a force (push) on that surface.
- If the force is great enough the surface gives way, such as in a balloon, when air forces the material to expand.
- If the surface does not give way, say as in a canister, gas pressure builds up.
- At sea level, it has been determined that the average pressure of the atmosphere is 101.325 kPa. This value is known as standard pressure or 1.0 atmosphere.
- Atmospheric pressure is measured by a barometer.
- The barometer was invented by Evangelista Torrecelli. He created a barometer utilizing liquid mercury in a long, inverted glass tube (test tube) placed in a pan of mercury.
- The height of the mercury would rise or fall depending on the atmospheric pressure changes. If the pressure dropped, the level of mercury would go down.
- The average air pressure at sea level is 101.325 kPa, which means that the height of the mercury would be 760 mm, also known as 760 torr.
- Therefore:
101.325 kPa = 760 mm Hg = 760 torr = 1 atm
Mercury Barometer

Conversions
- 99.0 kPa = _________ mm Hg

- 700 mm Hg = ___________ kPa

- 720 mm Hg = ____________ atm

- 1.43 atm = _____________ kPa

The Aneroid Barometer
- Because the mercury barometer has its disadvantages to its portability an aneroid barometer was developed.
- This barometer has a vacuum canister that expands or contracts as the pressure changes.
- The change in the shape of the canister causes a needle to move along a scale that reads the pressure.
- Very sensitive barometers measure altitude and are called altimeters.
The Four Gas Law Variables:
Volume, Temperature, Pressure and Moles
Volume
- All gases must be enclosed in a container.
- The three-dimensional space enclosed by the container walls is called volume (V).
- Volume in chemistry is usually measured in litres (L) or millilitres (mL). A litre is also called a cubic decimetre (dm3).
- A volume of 1 mL = 1 cm3.
Temperature
- All gases have a temperature, usually measured in degrees Celsius (°C), named after Anders Celsius. When the generalized variable of temperature is discussed, the symbol T is used.
- There is another temperature scale that is very important in gas behavior. It is called the Kelvin scale (K). Note that K does not have a degree sign and Kelvin is capitalized because this was a person's title (Lord Kelvin, his given name was William Thomson).
- All gas law problems must be done in Kelvin temperatures.
- Standard Temperature is defined as 0 °C or 273.15 K.
Pressure
- The molecules of gas hitting the walls of the container create gas pressure (P).
- There are three different units of pressure used in chemistry:
- atmospheres (atm)
- millimetres of mercury (mm Hg)
- pascals (Pa) or kilopascals (kPa)
- Standard Pressure is defined as one atm or 760.0 mm Hg or 101.325 kPa.
- Standard Temperature and Pressure is abbreviated to STP.
Amount of Gas
- The amount of gas present is measured in moles (mol) or in grams (g).
Boyle’s Law
- Robert Boyle investigated the relationship between pressure and volume in gases, while keeping the temperature constant.
- Boyle’s Law states that the volume of a quantity of gas, at a specific temperature, is inversely proportional to the pressure applied to the gas.
- This means that if the volume of a gas increases the pressure decreases.
- For example, if you had a syringe filled with air, there would be a certain amount of pressure inside the syringe. If you compressed the plunger, the volume of the gas would decrease, but the air pressure inside the cylinder would increase.
- Mathematically,

- A relationship such as this can be shown to have a constant, k.
![]()
- Inserting values, we can plot the inverse relationship between gas pressure and volume.

- As the volume approaches an infinitely small value, gas pressure reaches an infinitely large value.
- We can never get to zero volume nor zero pressure.
Boyle’s Law Problems
Using Boyle’s Law, we can calculate the final volume or pressure of a gas, given initial volume and pressure.
- A container has a volume of 10.0 L and the gas inside exerts a pressure of 75.0 kPa. If the volume of the container was changed to 2.00 L and the temperature was kept the same, calculate the new pressure exerted by the gas in the container.

- A syringe’s plunger is withdrawn, changing the volume of the gas from 35.75 cm3 to 83.90 cm3. If the final pressure is calculated to be 57.4 kPa what was the initial pressure of the gas, assuming that the temperature had not changed.

Charles’ Law
- J.A. Charles formulated a relationship between gas volume and the temperature, while keeping the pressure constant.
- He stated that the volume of a gas is directly proportional to the temperature of the gas, assuming the pressure remains constant.
- This means that as the volume of a gas decreases or gets smaller, the temperature of the gas also gets smaller.
- For example, if you blow up a balloon to a certain volume at room temperature and then expose the balloon to cold winter temperatures, the balloon's volume will decrease, just as the temperature had decreased.
- Mathematically,

- A relationship such as this can be shown to have a constant, k.

- Inserting values, we can plot the direct relationship between gas volume and temperature.

- As the volume approaches an infinitely small value, temperature, which is measured in Kelvins, reaches an infinitely small value.
- We can never get to zero volume nor zero temperature.
- A Kelvin degree is just another way of measuring temperature and is used in chemistry and physics for very low temperatures.
- The lowest possible temperature is at a point where no kinetic energy exists and therefore no molecular movement exists.
- This temperature is known to be at zero Kelvin (0 K) and is called absolute zero. ( Note: this is not written 0° K)
- Absolute zero is at –273.15 °C, therefore to measure the temperature in degrees Kelvin we use the formula: K = ° C + 273.15
- To calculate the temperature in °C we use the formula: ° C = K – 273.15

Temperature Conversions
Converting Kelvin to Celsius
25.0 °C = __________ K

25.0 K = ___________ °C

Note: For all gas problems that involve temperatures the unit must be in degrees Kelvin.
Charles’ Law Problems
- A certain gas occupies a volume of 35.5 L at a standard temperature of 0.00 °C. What volume will it occupy at 63.78 °C?
Given Information
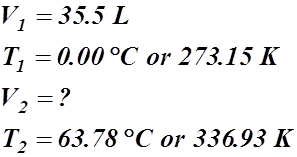
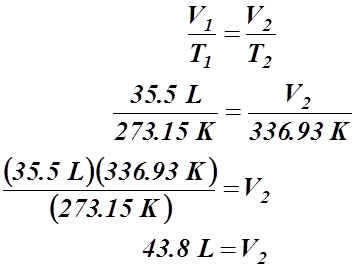
- A gas has a temperature of 67.4 °C when it is at a volume of 864 L. What will be its temperature if the volume is condensed to 10.0 L?
Given Information
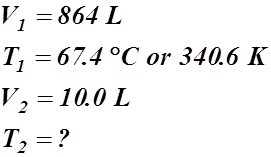
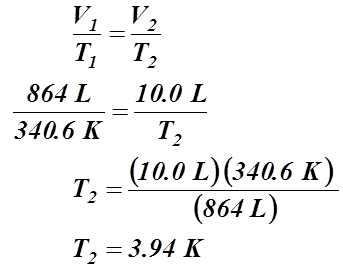
Gay-Lussac’s Law
- Gives the relationship between pressure and temperature when volume and amount are held constant.
- If the temperature of a container is increased, the pressure increases.
- The mathematical form of Gay-Lussac's Law is:

Problems
- 10.0 L of a gas is found to exert 97.0 kPa at 25.0 °C. What would be the required temperature (in Celsius) to change the pressure to standard pressure?


- 5.00 L of a gas is collected at 22.0°C and 745.0 mm Hg. When the temperature is changed to standard, what is the new pressure?


Avogadro's Law
- Gives the relationship between volume and amount when pressure and temperature are held constant. Amount is measured in moles.
- If the amount of gas in a container is increased, the volume increases.
- Suppose the amount is increased. This means there are more gas molecules and this will increase the number of impacts on the container walls. This means the gas pressure inside the container will increase, becoming greater than the pressure on the outside of the walls. This causes the walls to move outward. Since there is more wall space the impacts will lessen and the pressure will return to its original value.
- The mathematical form of Avogadro's Law is:

- This means that the volume-amount fraction will always be the same value if the pressure and temperature remain constant.
Problem: 5.00 L of a gas is known to contain 0.965 mol. If the amount of gas is increased to 1.80 mol, what new volume will result (at an unchanged temperature and pressure)?

Combined Gas Law
To derive the Combined Gas Law, do the following:
Step 1: Write Boyle's Law:
![]()
Step 2: Multiply by Charles Law:

Step 3: Multiply by Gay-Lussac's Law:

Step 4: Take the square root to get the combined gas law:

Problems
1. 2.00 L of a gas is collected at 25.0°C and 745.0 mm Hg. What is the volume at STP?


2. A container is reduced to a volume of 125 cm3 when a temperature of –75.00 °C is reached. If the pressure changes from 1.20 atm to 852 torr and the initial temperature was 20.00 °C, calculate the initial volume.


Molar Volume
- The molar volume is the volume occupied by one mole of ideal gas at STP or SATP (RTP).
- It is the volume of ANY ideal gas at Standard Temperature and Pressure (STP) or Standard Ambient Temperature and Pressure (SATP or RTP).
- Its value is:
STP:  or SATP (RTP):
or SATP (RTP): 
: T = 0 °C : T = 25 °C
Example #1: You have 2.00 L of dry H2 at STP.
- How many moles is this?
- What is the mass of the hydrogen gas?
Solution:
a) If 22.4 L of gas equals 1 mol of gas, we can set up a simple ratio:

b)

Example #2: 0.250 mol of HCl(g) will occupy how many litres at STP?
Solution:

Example #3: What is the molar volume at 576 K?
Solution: Since 576 K is not a standard temperature, we must create a ratio to find the new volume.

Ideal Gas Law
- We can combine all gas laws into one convenient expression:
![]()
where
P = pressure in kPa
V = volume in L
n = moles of gas in mol
T = temperature in K
R = Universal Gas Constant = 8.314 kPa×L×mol–1×K–1
or 
Example #1: What mass of hydrogen gas can be produced if the gas occupies a volume of 50.0 mL at 20.00 °C and 94.5 kPa?
Given Information:
m = ?
V = 50.0 mL or 0.0500 L
T = 20.00 °C or 293.15 K
P = 94.5 kPa
To solve for mass we need the formula:
m = nM
Since number of moles is unknown, we need to use the given information to solve for moles.

Now, calculate for mass:

Example #2: A balloon has a volume of 10 000 L at 100 kPa and 20.00 °C. If one was to fill this balloon with helium, how many moles of helium would be required?
Given:
V = 10 000 L
P = 100 kPa
T = 20.00 °C or 293.15 K
n = ?

Example #3: A storage tank contains 2.65 kg of methane gas at 735.2 kPa and 25.00 °C. What is the tank’s volume?
Given:
m = 2.65 kg or 2.65 x 103 g
P = 735.2 kPa
T = 25.00 °C or 298.15 K
V = ?


Example #4: If 38.5 g of nitrogen gas is found in a container with a volume of 15.27 L and 1.19 atm, what is the temperature in degrees Celsius?
Given:
m = 38.5 g
V = 15.27 L
P = 1.19 atm or 121 kPa
T = ? °C


Dalton’s Law of Partial Pressure
- John Dalton’s law of partial pressure states that the total pressure exerted by a mixture of gases is the sum of the partial pressures of each gas in the container.
![]()
Example: A container has Gas A at a pressure of 1.25 atm, Gas B at a pressure of 102 kPa and Gas C at a pressure of 720 mm Hg. What is the total pressure, in kPa, inside the container?

Example: The total pressure inside a container is 140 kPa. If 7 molecules of Gas A, 2 molecules of Gas B and 1 molecule of Gas C exist, calculate the pressure exerted by each gas.
Total molecules = 10 molecules
Gas A: 7 molecules or 70 %
Gas B: 2 molecules or 20 %
Gas C: 1 molecule or 10 %
Gas A: 70 % of 140 kPa = 98.0 kPa
Gas B: 20 % of 140 kPa = 28.0 kPa
Gas C: 10 % of 140 kPa = 14.0 kPa
Ideal Gases vs Real Gases
- We have assumed that all gases obey the Ideal Gas Law (PV = nRT).
- In an “Ideal” gas, molecules have no volume and no intermolecular forces. This assumption must be made in order to make the Ideal Gas Law formula work in all cases.
- While the Ideal Gas Law does a very good job of predicting gas behavior, it's not perfect.
- Real gases differ in two major ways from an ideal gas
- Particles in a real gas have volume.
- Particles in a real gas attract each other, especially when they are condensed.
Summary
|
Temperature |
Pressure |
Molar Volume |
STP |
273.15 K |
101.325 kPa |
|
SATP |
273.15 K |
0.1 MPa |
|
- Boyle's Law:

- Charles’ Law:

- Gay-Lussac’s Law:

- Avogadro's Law:

- Combined Gas Law:

- Ideal Gs Law: PV = nRT
- R =

- Dalton’s Law of Partial Pressure:
![]()
Gas Law Stoichiometry
- In our stoichiometry unit, we looked at four different types of questions:
Mole to Mole |
Mole to Mass |
Mass to Mole |
Mass to Mass |
Given – moles Required - moles |
Given – moles Required - mass |
Given –mass |
Given – |
- To solve these questions, we look at our given information, looked at our required information and then decided on the steps to take:


![]()
![]()

- Now, we are going to include volume to stoichiometry questions. We use the Ideal Gas Law to do this:

Problems
- What volume of CO2(g) is produced at 94.5 kPa and 115.5 °C in the exhaust of a car if 100 g of gasoline (C8H18(g)) are burned?

![]()



- How many moles of sodium must react with H2O(l) to produce 250 mL of H2(g) at 23.6 °C and 102.6 kPa?
2 Na(s) + 2 HOH(l) ® H2(g) + 2 NaOH(aq)
n = ? V = 0.250 L
T = 23.6 °C or 296.8 K
P = 102.6 kPa


- If 17.8 L of hydrogen, at 22.5 °C and 21.4 kPa, react with nitrogen to produce 22.7 L of ammonia at 33.9 kPa, what’s the temperature of the ammonia (in °C)?
3 H2(g) + N2(g) ® 2 NH3(g)
V = 17.8 L V = 22.7 L
T = 22.5 °C or 295.7 K P = 33.9 kPa
P = 21.4 kPa T = ? °C



- What volume of carbon monoxide gas could be produced at STP by the incomplete combustion of 50.0 kmol of coal (assume pure carbon)?
2 C(s) + O2(g) ® 2 CO(g)
![]() V = ?
V = ?
T = 273.15 K
P = 101.325 kPa


Source : http://www.archbishopjordan.ab.ca/Science%20Notes/chemistry%2020/Chem%2020%20Unit%2007%20Overhead%20Notes_Gases.doc
Web site link: http://www.archbishopjordan.ab.ca/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Gases
Gases
Gases
This is the right place where find the answers to your questions like :
What is Gases? What does Gases mean ? Which is the meaning of Gases?
Gases chemistry notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us

